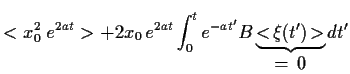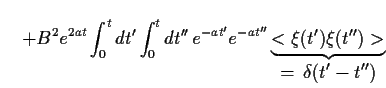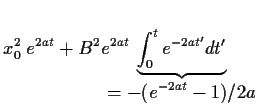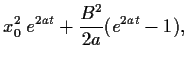Nächste Seite: Stochastische Differentialgleichungen
Aufwärts: Markov-Prozesse
Vorherige Seite: Fokker-Planck-Gleichung
Inhalt
Eine Alternative zur Behandlung von Markov-Prozessen
mit Hilfe von
Fokker-Planck-Gleichungen
ist der Kalkül der
stochastische Differentialgleichungen.
Als einfaches Beispiel
wollen wir in diesem Abschnitt die Langevin-Gleichung
diskutieren.
Diese ist eine stochastische Differentialgleichung
der Gestalt
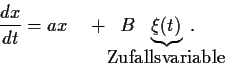 |
(34) |
Stochastisch heißt diese Diferentialgleichung,
da hierin 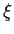 als eine normalverteilte Zufallsvariable
angenommen wird, mit Mittelwert
als eine normalverteilte Zufallsvariable
angenommen wird, mit Mittelwert
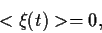 |
(35) |
und Kovarianz
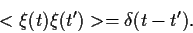 |
(36) |
Mit 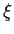 ist auch
ist auch 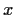 eine Zufallsvariable.
In der ursprünglichen Anwendung der Langevin-Gleichung in der Physik
steht hierbei die Zufallsvariable
eine Zufallsvariable.
In der ursprünglichen Anwendung der Langevin-Gleichung in der Physik
steht hierbei die Zufallsvariable 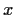 für die Geschwindigkeit
eines Teilchen,
welches durch eine Reibungskraft
für die Geschwindigkeit
eines Teilchen,
welches durch eine Reibungskraft 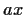 mit
mit 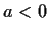 abgebremst wird
und dem Einfluß von Zufallskräften
abgebremst wird
und dem Einfluß von Zufallskräften 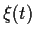 ausgesetzt ist.
Bei der Herleitung der Black-Scholes-Formel
wird uns eine etwas allgemeinere Gleichung begegnen,
bei der
ausgesetzt ist.
Bei der Herleitung der Black-Scholes-Formel
wird uns eine etwas allgemeinere Gleichung begegnen,
bei der 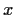 beispielsweise den Aktienkurs
und
beispielsweise den Aktienkurs
und 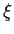 die Änderung des Aktienkurses
representieren.
die Änderung des Aktienkurses
representieren.
Nehmen wir eine Zufallsrealisierung
von 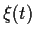 als gegeben an, so können
wir naiv
(ohne uns ersteinmal über die Existenz des Integrals Gedanken zu machen)
eine Lösung von Gl. (34) angeben,
als gegeben an, so können
wir naiv
(ohne uns ersteinmal über die Existenz des Integrals Gedanken zu machen)
eine Lösung von Gl. (34) angeben,
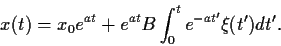 |
(37) |
Da Gl. (37) 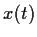 als eine Linearkombination
der
als eine Linearkombination
der 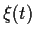 darstellt
und eine Summe von normalverteilten Variablen
wieder normalverteilt ist,
ist daher in diesem Falle mit
darstellt
und eine Summe von normalverteilten Variablen
wieder normalverteilt ist,
ist daher in diesem Falle mit 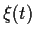 auch
auch 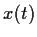 normalverteilt.
normalverteilt.
Für den Mittelwert
von 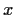 zur Zeit
zur Zeit 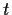 unter der Anfangsbedingung
unter der Anfangsbedingung
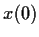 =
= 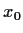 folgt
unter Benutzung von Gl. (35),
folgt
unter Benutzung von Gl. (35),
Dies entspricht der Gl. (32)
für den Mittelwert der Lösung (31)
der linearen Fokker-Planck-Gleichung
(30).
Ähnlich folgt für den Erwartungwerts von 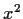 zur Zeit
zur Zeit 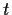 unter Verwendung von Gl. (35) und Gl. (36),
unter Verwendung von Gl. (35) und Gl. (36),
und daher für die Varianz,
![\begin{displaymath}
V[x(t)]
= <x^2(t)>
- <\!x(t)\!>^2
=
\frac{B^2}{2a} (e^{2at}-1)
.
\end{displaymath}](img160.gif) |
(40) |
Dies entspricht der Gl. (33)
für die Varianz der Lösung (31)
der linearen Fokker-Planck-Gleichung
(30).
Eine Gaußverteilung ist durch Mittelwert und Varianz
bereits vollständig beschrieben.
Nehmen wir also die 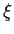 und damit nach Gl. (37)
auch die
und damit nach Gl. (37)
auch die 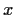 ,
als normalverteilt an,
so ist die Wahrscheinlichkeitsverteilung der
,
als normalverteilt an,
so ist die Wahrscheinlichkeitsverteilung der 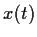 durch Gl. (38)
und Gl. (40)
vollständig bestimmt.
Damit ist also die Langevin-Gleichung (34)
equivalent zu der
linearen Fokker-Planck-Gleichung
(30).
durch Gl. (38)
und Gl. (40)
vollständig bestimmt.
Damit ist also die Langevin-Gleichung (34)
equivalent zu der
linearen Fokker-Planck-Gleichung
(30).




Nächste Seite: Stochastische Differentialgleichungen
Aufwärts: Markov-Prozesse
Vorherige Seite: Fokker-Planck-Gleichung
Inhalt
Joerg_Lemm
2000-02-25
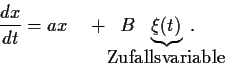
![]() als gegeben an, so können
wir naiv
(ohne uns ersteinmal über die Existenz des Integrals Gedanken zu machen)
eine Lösung von Gl. (34) angeben,
als gegeben an, so können
wir naiv
(ohne uns ersteinmal über die Existenz des Integrals Gedanken zu machen)
eine Lösung von Gl. (34) angeben,
![]() zur Zeit
zur Zeit ![]() unter der Anfangsbedingung
unter der Anfangsbedingung
![]() =
= ![]() folgt
unter Benutzung von Gl. (35),
folgt
unter Benutzung von Gl. (35),