



Nächste Seite: Optionspreise nach Black-Scholes
Aufwärts: Markov-Prozesse
Vorherige Seite: Stochastische Differentialgleichungen
Inhalt
Das stochastische Differential
einer beliebigen von 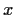 -abhängigen Funktion
-abhängigen Funktion ![$f[x(t),t]$](img180.gif) ,
läßt sich mit den Beziehungen (46)
und (49)
nun ebenfalls berechnen.
Dazu machen wir eine Taylorentwicklung
bis zur ersten Ordnung in
,
läßt sich mit den Beziehungen (46)
und (49)
nun ebenfalls berechnen.
Dazu machen wir eine Taylorentwicklung
bis zur ersten Ordnung in 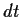 ,
das heißt also bis zur zweiten Ordnung in
,
das heißt also bis zur zweiten Ordnung in 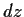 ,
,
Diese Beziehung ist bekannt als Itô's Lemma.
Sie ist von grundlegender Bedeutung
für den Itô-Kalkül
und daher auch für die
klassische Herleitung der Black-Scholes-Formel.
Itô's Lemma kann auch dazu verwendet werden, die
Äquivalenz
einer stochastische Differentialgleichung
zu einer Fokker-Planck-Gleichung
zu zeigen.
Bilden wir den Erwartungswert
der Gl. (50)
unter
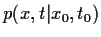 und dividieren durch
und dividieren durch 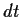 ,
so erhalten wir für eine beliebige,
nicht explizit zeitabhängige Funktion
,
so erhalten wir für eine beliebige,
nicht explizit zeitabhängige Funktion ![$f[x(t)]$](img186.gif) ,
,
Wir haben hierbei benutzt, daß Im Itô-Kalkül 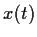 zur Zeit
zur Zeit 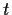 von der zukünftigen Änderung
von der zukünftigen Änderung
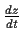 =
= 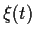 unabhängig ist.
Daher faktorisiert der erste Term
und verschwindet dann wegen
unabhängig ist.
Daher faktorisiert der erste Term
und verschwindet dann wegen 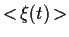 = 0.
Das Wegfallen des
= 0.
Das Wegfallen des 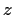 -abhängigen Terms
ist also bedingt durch die Definition der ``Riemann''-Summen
in der Definition des Itô-Integrals,
bei der immer der Funktionswert am Anfang des Teilintervalls
zur Bildung der Teilsummen gewählt wird.
Dies korrespondiert zu der Markov-Eigenschaft.
Einsetzen der Definition des Erwartungswertes
liefert dann
-abhängigen Terms
ist also bedingt durch die Definition der ``Riemann''-Summen
in der Definition des Itô-Integrals,
bei der immer der Funktionswert am Anfang des Teilintervalls
zur Bildung der Teilsummen gewählt wird.
Dies korrespondiert zu der Markov-Eigenschaft.
Einsetzen der Definition des Erwartungswertes
liefert dann
Durch partielle Integration
erhalten wir daraus bei verschwindenden Randtermen,
Da wir ![$f[x]$](img196.gif) beliebig wählen können,
folgt daraus
beliebig wählen können,
folgt daraus
![\begin{displaymath}
\frac{d}{dt} p(x,t\vert x_0,t_0)
=
-
\frac{\partial }{\parti...
...2 }{\partial x^2}
\left(B^2[x,t] p(x,t\vert x_0,t_0)\right)
,
\end{displaymath}](img197.gif) |
(53) |
also gerade die allgemeine Fokker-Planck-Gleichung (20).
Damit folgt die Äquivalenz der allgemeinen
stochastischen Differentialgleichung (41)
(im Itô-Kalkül)
mit der Fokker-Planck-Gleichung (20).
Bei der Herleitung dieser Äquivalenz
haben wir an zwei Stellen auf den
Itô-Kalkül Bezug genommen:
Einmal durch Benutzung der Itô-Formel,
zum anderen durch
das Wegfallen des ersten Terms in Gl. (51).
Im Stratonovich-Kalkül
findet man, daß eine
stochastische Differentialgleichung der Form (41),
interpretiert im Sinne von Stratonovich
[und daher nicht equivalent zu einer im Itô-Kalkül interpretierten
Gl. (41)]
korrespondiert zu
einer Fokker-Planck-Gleichung
der Form [7,9]
Zum Abschluß sei nochmal betont, daß die Fokker-Planck-Gleichung
eine normale, und keine stochastische
partielle Differentialgleichung darstellt.
Eine Fokker-Planck-Gleichung ist daher stets eindeutig definiert
und von der Wahl einer Definition
des stochastischen Integrals nicht betroffen.
Zu ihr korrespondieren aber,
in Abhängigkeit von der Definition des stochastischen Integrals,
unterschiedliche stochastische Differentialgleichungen,
Abbildung
1
faßt die diskutierten
Ansätze zur Behandlung von Markov-Prozessen
nochmals zusammen.
Abbildung 1:
Überblick über Ansätze zur Behandlung von Markov-Prozessen
![\begin{figure}\begin{eqnarray}
&
\mbox{\bf Markov-Proze\ss}
&\nonumber &
\dis...
...{\partial x}} B[x,t]
\right)dt + B[x,t] dz
&\nonumber
\end{eqnarray}\end{figure}](img201.gif) |




Nächste Seite: Optionspreise nach Black-Scholes
Aufwärts: Markov-Prozesse
Vorherige Seite: Stochastische Differentialgleichungen
Inhalt
Joerg_Lemm
2000-02-25
![]() -abhängigen Funktion
-abhängigen Funktion ![]() ,
läßt sich mit den Beziehungen (46)
und (49)
nun ebenfalls berechnen.
Dazu machen wir eine Taylorentwicklung
bis zur ersten Ordnung in
,
läßt sich mit den Beziehungen (46)
und (49)
nun ebenfalls berechnen.
Dazu machen wir eine Taylorentwicklung
bis zur ersten Ordnung in ![]() ,
das heißt also bis zur zweiten Ordnung in
,
das heißt also bis zur zweiten Ordnung in ![]() ,
,
![]() und dividieren durch
und dividieren durch ![]() ,
so erhalten wir für eine beliebige,
nicht explizit zeitabhängige Funktion
,
so erhalten wir für eine beliebige,
nicht explizit zeitabhängige Funktion ![]() ,
,
![$\displaystyle \int \!dx
f[x] \frac{d}{dt} p(x,t\vert x_0,t_0)$](img191.gif)
![$\displaystyle \int \!dx p(x,t\vert x_0,t_0)
A[x,t] \frac{\partial f}{\partial x}$](img192.gif)
![$\displaystyle + \frac{1}{2}
\int \!dx p(x,t\vert x_0,t_0)
B^2[x,t] \frac{\partial^2 f}{\partial x^2}
.$](img193.gif)
![$\displaystyle \int \!dx
f[x] \frac{d}{dt} p(x,t\vert x_0,t_0)$](img191.gif)
![$\displaystyle -\int \!dx f[x]
\frac{\partial }{\partial x} \Big(A[x,t]p(x,t\vert x_0,t_0)\Big)$](img194.gif)
![$\displaystyle + \frac{1}{2}
\int \!dx f[x]
\frac{\partial^2 }{\partial x^2}
\left(B^2[x,t] p(x,t\vert x_0,t_0)\right)
.$](img195.gif)
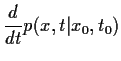
![$\displaystyle -
\frac{\partial }{\partial x}
\left[
\left(A[x,t]+\frac{1}{2} B[x,t] \frac{d}{dx} B[x,t] \right)p(x,t\vert x_0,t_0)
\right]$](img199.gif)
![$\displaystyle + \frac{1}{2}
\frac{\partial^2 }{\partial x^2}
\left[B^2[x,t] p(x,t\vert x_0,t_0)\right]
.$](img200.gif)