



Nächste Seite: Fokker-Planck-Gleichung
Aufwärts: Markov-Prozesse
Vorherige Seite: Chapman-Kolmogorov-Gleichung
Inhalt
Wir betrachten nun
Gl. (6)
für
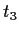 =
= 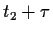 mit kleinen Zeitdifferenzen
mit kleinen Zeitdifferenzen 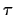 ,
um im Limes
,
um im Limes
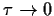 eine Gleichung für die Zeitableitung
eine Gleichung für die Zeitableitung
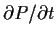 zu bekommen.
Wir erhalten
zu bekommen.
Wir erhalten
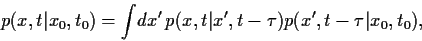 |
(7) |
für
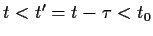 .
Wenn wir nun
.
Wenn wir nun
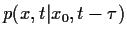 für kleine
für kleine 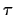 taylorentwickeln wollen,
müssen wir berücksichtigen,
daß
wegen der Normierungsbedingung
taylorentwickeln wollen,
müssen wir berücksichtigen,
daß
wegen der Normierungsbedingung
 |
(8) |
also
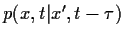 auch von allen
auch von allen
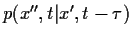 mit
mit
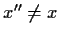 abhängt.
Schreiben wir also
abhängt.
Schreiben wir also
 |
(9) |
(wobei wir die rechte Seite auch für unnormierte 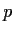 verwenden könnten),
so erhalten wir durch eine Taylorentwicklung
in
verwenden könnten),
so erhalten wir durch eine Taylorentwicklung
in 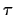 =
= 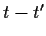 ,
,
Hierbei bezeichnet
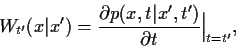 |
(11) |
die momentane Übergangsrate von 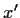 nach
nach 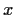 pro Zeiteinheit
und der Term
pro Zeiteinheit
und der Term
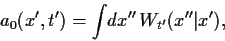 |
(12) |
sorgt dafür,
daß die Normierungsbedingung
auch für das
taylorentwickelte 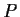 gültig bleibt.
Wir setzten hier die Existenz von
gültig bleibt.
Wir setzten hier die Existenz von 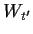 voraus,
bemerken jedoch, daß im allgemeinen Gl. (10)
nicht gelten muß [7,9].
voraus,
bemerken jedoch, daß im allgemeinen Gl. (10)
nicht gelten muß [7,9].
Setzen wir jetzt für kleines 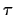 die Taylorentwicklung (10)
in die Chapman-Kolmogorov-Gleichung
Gl. (7) ein,
so finden wir für
die Taylorentwicklung (10)
in die Chapman-Kolmogorov-Gleichung
Gl. (7) ein,
so finden wir für
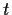 =
= 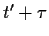 ,
,
Bringen wir den Term
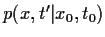 auf die linke Seite,
teilen durch
auf die linke Seite,
teilen durch 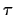 und bilden den Grenzübergang
und bilden den Grenzübergang
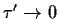 ,
so erhalten wir [für in
,
so erhalten wir [für in 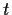 stetige
stetige
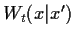 ,
,
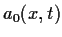 ,
,
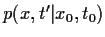 , also z.B.
, also z.B.
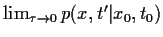 =
=
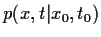 ]
die sogenannte
Mastergleichung
]
die sogenannte
Mastergleichung
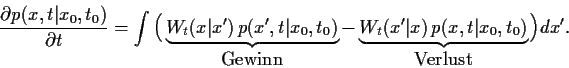 |
(14) |
Die Gleichung läßt sich also als Bilanzgleichung verstehen,
in der die Änderung von
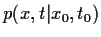 gegeben ist in der Form
Gewinn- minus Verlustterm
bzw. Zufluß- minus Abflußterm.
Die Fall
gegeben ist in der Form
Gewinn- minus Verlustterm
bzw. Zufluß- minus Abflußterm.
Die Fall
 bedeuted hier also,
daß Mehrfachterme,
wie z.B. einen Wechsel
von
bedeuted hier also,
daß Mehrfachterme,
wie z.B. einen Wechsel
von 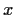 nach
nach 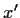 und anschließend wieder zurück nach
und anschließend wieder zurück nach 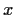 ,
nicht berücksichtigt werden.
,
nicht berücksichtigt werden.
Für eine diskrete 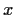 -Variable
wird Gl. (14)
zu,
-Variable
wird Gl. (14)
zu,
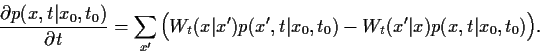 |
(15) |
Analog erhält man für diskrete Zeiten
eine Differenzengleichung
(unter der Voraussetzung, daß pro betrachtetem Zeitintervall nur ein
Übergang gemäß der gewählten Übergangswahrscheinlichkeiten
stattfindet).
In abstrakterer Form läßt sich
die Mastergleichung (14)
schreiben als
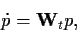 |
(16) |
wobei
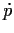 =
=
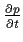 und
und
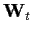 einen linearen Operator
darstellt
mit Matrixelementen,
einen linearen Operator
darstellt
mit Matrixelementen,
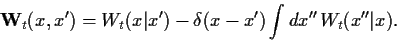 |
(17) |
Gl. (16)
hat für zeitunabhängiges
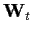 =
= 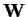 die formale Lösung
die formale Lösung
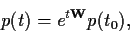 |
(18) |
die aber in der Regel nicht benutzt werden kann
um 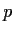 zu finden.
Bei diskreten
zu finden.
Bei diskreten 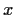 wird
wird 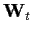 eine endlichdimensionale Matrix.
Die folgenden speziellen Eigenschaften
von
eine endlichdimensionale Matrix.
Die folgenden speziellen Eigenschaften
von 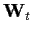 lassen sich leicht überprüfen
lassen sich leicht überprüfen
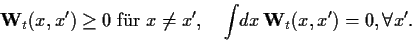 |
(19) |
Für daraus sich ergebende Folgerungen siehe zum Beispiel
[9].




Nächste Seite: Fokker-Planck-Gleichung
Aufwärts: Markov-Prozesse
Vorherige Seite: Chapman-Kolmogorov-Gleichung
Inhalt
Joerg_Lemm
2000-02-25
![]() =
= ![]() mit kleinen Zeitdifferenzen
mit kleinen Zeitdifferenzen ![]() ,
um im Limes
,
um im Limes
![]() eine Gleichung für die Zeitableitung
eine Gleichung für die Zeitableitung
![]() zu bekommen.
Wir erhalten
zu bekommen.
Wir erhalten

![]() die Taylorentwicklung (10)
in die Chapman-Kolmogorov-Gleichung
Gl. (7) ein,
so finden wir für
die Taylorentwicklung (10)
in die Chapman-Kolmogorov-Gleichung
Gl. (7) ein,
so finden wir für
![]() =
= ![]() ,
,
![$\displaystyle \int\!dx^\prime
\Big(
[1-\tau a(x^\prime,t^\prime)]\delta(x-x^\...
...e)
+ \tau W_{t^\prime}(x\vert x^\prime)
\Big)
p(x^\prime,t^\prime\vert x_0,t_0)$](img67.gif)
![$\displaystyle p(x,t^\prime\vert x_0,t_0)[1-\tau^\prime a(x,t^\prime)]
+ \tau
\int\!dx^\prime W_{t^\prime}(x\vert x^\prime)p(x^\prime,t^\prime\vert x_0,t_0)$](img68.gif)
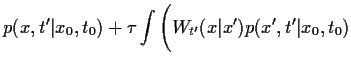
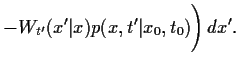
![]() -Variable
wird Gl. (14)
zu,
-Variable
wird Gl. (14)
zu,