Nächste Seite: Abschätzung des Einflusses von
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Erwartungswertprinzip und ``No-Arbitrage''-Prinzip
Inhalt
Betrachten wir nun die Vermögensbilanz
des Schreibers (Long-Position)
einer
europäischen
Call-Option
mit Ausübungspreis (strike price) 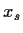 ,
,
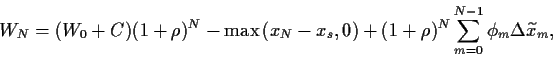 |
(19) |
wobei wir berücksichtigt haben, daß die Optionsprämie bereits bei Abschluß,
also zur Zeit  fällig wird.
fällig wird.
Aus der Bedingung für einen fairen Preis
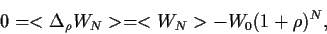 |
(20) |
folgt
für den Optionspreis
(dem in dem realistischen Fall, in dem keine risikofreie
Hedging-Strategie möglich ist,
noch eine Risikozulage zugeschlagen werden muß),
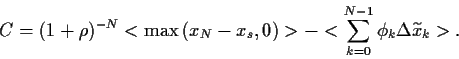 |
(21) |
Hierbei ist
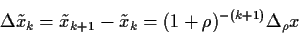 |
(22) |
mit
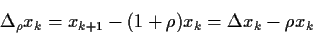 |
(23) |
und
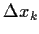 =
= 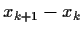 .
Analog zu den relativen Änderungen
.
Analog zu den relativen Änderungen
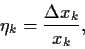 |
(24) |
definieren wir nun
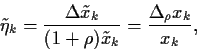 |
(25) |
welches zu 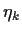 in der Beziehung steht
in der Beziehung steht
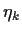 =
=
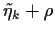 .
.
Wir nehmen nun an, daß die
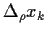 bzw.
bzw. 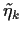 =
=
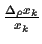 unabhängig normalverteilt sind.
In beiden Fälen können wir die Kurse
unabhängig normalverteilt sind.
In beiden Fälen können wir die Kurse 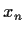 durch die unabhängigen Zufallsgrößen
durch die unabhängigen Zufallsgrößen
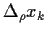 bzw.
bzw. 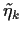 ausdrcken.
Für
ausdrcken.
Für
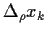 erhalten wir beispielsweise durch Iteration,
analog zu
erhalten wir beispielsweise durch Iteration,
analog zu
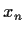 =
=
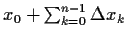
![$\left[
= x_0 + \sum_{k=0}^{n-1} \left(\Delta_\rho x_k+\rho x_k\right)
\right]$](img114.gif) ,
,
Dies bedeutet,
daß 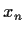 nur von den
nur von den
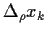 mit
mit 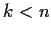 abhängt.
Dasselbe gilt daher für die Zahl der gehaltenen Aktien
abhängt.
Dasselbe gilt daher für die Zahl der gehaltenen Aktien 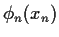 ,
die nur vom bekannten aktuellen Kurs
,
die nur vom bekannten aktuellen Kurs 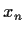 ,
aber nicht von der noch unbekannten zukünftigen
Kursänderung
,
aber nicht von der noch unbekannten zukünftigen
Kursänderung
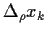 abhängt.
Die Unabhängigkeit der
abhängt.
Die Unabhängigkeit der 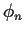 von
von
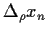 ,
bedeutet
,
bedeutet
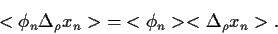 |
(27) |
In der Tat, folgt diese Beziehung direkt aus
Gleichung (26) und
der Unabhängigkeit der
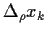 , d.h.
einer faktorisierenden gemeinsamen Wahrscheinlichkeit
, d.h.
einer faktorisierenden gemeinsamen Wahrscheinlichkeit
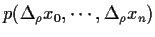 =
=
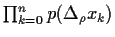 ,
,
Ähnlich wie (26) läßt sich 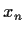 auch durch
die bis zum Zeitpunkt
auch durch
die bis zum Zeitpunkt 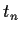 bereits aufgetretenen
bereits aufgetretenen
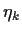 bzw.
bzw. 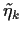 ausdrücken
ausdrücken
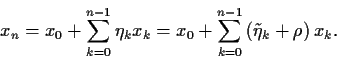 |
(29) |
Expliziter erhalten wir durch Iteration,
für 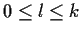 ,
und ebenso für die
,
und ebenso für die 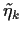 ,
,
Für den Fall, daß die 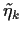 als unabhängige Zufallsvariablen aufgefaßt werden
gilt daher,
als unabhängige Zufallsvariablen aufgefaßt werden
gilt daher,
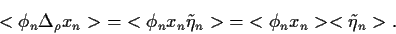 |
(32) |
Unter der Annahme
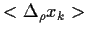 =
= 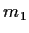 =
= 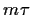 = 0
bei unabhängigen Zufallsvariablen
= 0
bei unabhängigen Zufallsvariablen
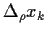 ,
bzw.
,
bzw.
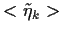 =
= 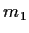 =
= 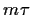 = 0
bei unabhängigen
= 0
bei unabhängigen 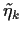 ,
fällt also der ganze ``Tradingterm''
,
fällt also der ganze ``Tradingterm''
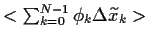 aus Gl. (21) heraus.
aus Gl. (21) heraus.




Nächste Seite: Abschätzung des Einflusses von
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Erwartungswertprinzip und ``No-Arbitrage''-Prinzip
Inhalt
Joerg_Lemm
2000-02-02
![]() ,
,
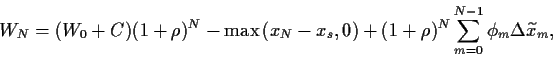
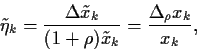
![]() bzw.
bzw. ![]() =
=
![]() unabhängig normalverteilt sind.
In beiden Fälen können wir die Kurse
unabhängig normalverteilt sind.
In beiden Fälen können wir die Kurse ![]() durch die unabhängigen Zufallsgrößen
durch die unabhängigen Zufallsgrößen
![]() bzw.
bzw. ![]() ausdrcken.
Für
ausdrcken.
Für
![]() erhalten wir beispielsweise durch Iteration,
analog zu
erhalten wir beispielsweise durch Iteration,
analog zu
![]() =
=
![]()
![]() ,
,
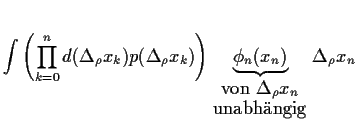
![$\displaystyle \underbrace{
\left[
\int \left( \prod_{k=0}^{n-1} d(\Delta_\rho x...
... p(\delta_\rho x_n)
\Delta_\rho x_n
\right]
}_{\displaystyle <\Delta_\rho x_n>}$](img130.gif)