Use the finite-difference method (2.10) to solve the wave equation for a vibrating string:
with the boundary conditions
Assume that the initial position and velocity are
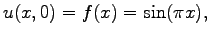
and
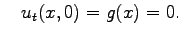
Other parameters are:
| Space interval |
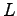 =10
=10 |
| Space discretization step |
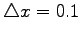
|
| Time discretization step |
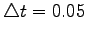
|
| Amount of time steps |
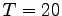
|
First one can find the d'Alambert solution. In the case of zero initial velocity Eq. (2.8) becomes
i.e., the solution is just a sum of a travelling waves with initial form, given by
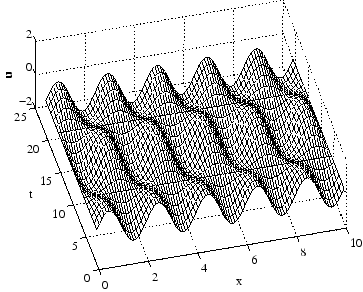
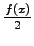 . Numerical solution of (2.17) is shown on Fig. (2.1.3).
. Numerical solution of (2.17) is shown on Fig. (2.1.3).
Figure 2.4:
Space-time evolution of the initial distribution
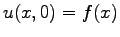 ,
,
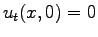 .
.
 |
Gurevich_Svetlana
2008-11-12
