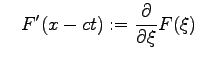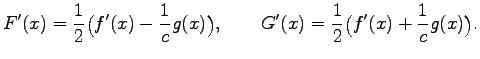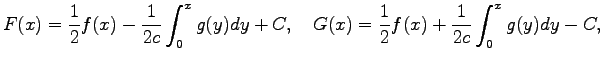Consider now an initial value problem for Eq. (2.2):
To write down the general solution of the initial value problem for (2.2) one needs to exspress the arbitrary function 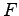 and
and 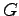 in terms of initial data
in terms of initial data 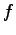 and
and 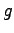 . Using the relation
. Using the relation
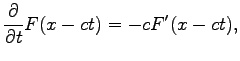
where
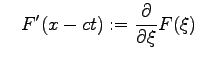
one becomes:
After differentiation of the first equation with respect to 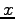 one can solve the system in terms of
one can solve the system in terms of 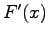 and
and 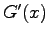 , i.e.,
, i.e.,
Hence
where the integration constant 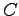 is chosen in such a way that the initial condition
is chosen in such a way that the initial condition
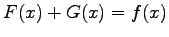 is fullfield. Alltogether one obtains:
is fullfield. Alltogether one obtains:
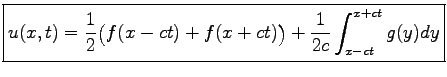 |
(2.8) |
Gurevich_Svetlana
2008-11-12
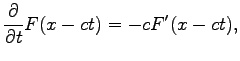 where
where