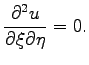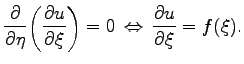The wave equation for the scalar 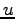 in the one dimensional case reads
in the one dimensional case reads
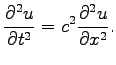 |
(2.2) |
The general solution of Eq. (2.2) was first derived by Jean le Rond d'Alembert. Let us introduce new coordinates
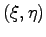 by use of the transformation
by use of the transformation
 |
(2.3) |
In the new coordinate system Eq. (2.2) becomes
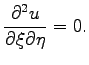 |
(2.4) |
This equation means that the function 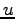 remains constant along the curves (2.3), i.e., (2.3) are characteristic curves of the wave equation (2.2). Moreover, one can see that the derivative
remains constant along the curves (2.3), i.e., (2.3) are characteristic curves of the wave equation (2.2). Moreover, one can see that the derivative
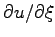 does not depends on
does not depends on 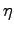 , i.e.,
, i.e.,
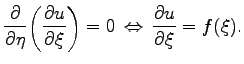 |
(2.5) |
After integration with respect to 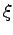 one obtains
one obtains
where 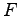 is the primitive function of
is the primitive function of 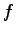 and
and 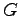 is the ''constant`` of integration, in general the function of
is the ''constant`` of integration, in general the function of 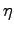 .
Turning back to the coordinates
.
Turning back to the coordinates 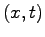 one obtains the general solution of Eq. (2.2)
one obtains the general solution of Eq. (2.2)
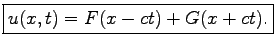 |
(2.6) |
Subsections
Gurevich_Svetlana
2008-11-12
![]() in the one dimensional case reads
in the one dimensional case reads