Reaction Diffusion Systems

Further details with respect to the treatment of reaction diffusion systems

Observing nature shows that many temporal and spatial structures are not formed by the outside, but rather by the respective system itself. To study these self-organizing processes is the subject of the research group "Pattern Formation in dissipative Systems".

Having a closer look on these self-organizing phenomenons it turns out that a lot of them can be well described by a class of reaction-diffusion equations of the following types: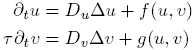

These equations are describing the temporal developments of the two distributions u(x,t) und v(x,t). Their dynamics are determined by a local acting reaction term and by a spatial coupling via a diffusion term. In this way the complex behaviour of many bilogical, chemical, physical and other self-organizing systems can be described. The pulse spreading on a chickens' retina, the Belousov-Zhabotinsky-reaction or dc gas discharge systems may serve as an example for this.

Important aspects of these systems are potential bistabilities already in a state of stationary homogenous structures, spatial, temporal and spatio-temporal inhomogeneous structures including chaotic behaviour.

In the case of stationary structures, the second component v, the so-called inhibitor, gets a stabilizing effect. This stabilizing effect shows to its best advantage if he is fast and if he won't be spread by diffusion. A slowing down of the component v will typically lead to a temporal structure formation (e.g. pulses, running waves), an increased diffusion forming spatial patterns (e.g. periodic Turing-structures, localized filaments). A simultaneous lesion of both conditions facilitates even more complex structures (such as breathing filaments, oscillating areas embedded in an environment of stationary periodical patterns, spatio-temporal chaos). Furthermore exist structure elements containing the properties of well localized particles of well-defined size which interact with each other and also with the boundary. They also can either be destroyed or created. The following image gives examples for some structures of such a two-component-system (binary system).

Self-organizing spatial structures as a solution of an activator-inhibitor-reaction-diffusion-system.

The numerical an analytic treatment of these activator-inhibitor-reaction-diffusion-sytsems is done in order to examine the basic mechanisms of natural pattern formation with the aim to be able to predict the principle phenomenons theoretically. Over and above that they are used to interpret experiments done on plasma systems and semiconductors (please also have a look at the following fields of work: "DC Gas Discharge" and "AC Gas Discharge".

Quasi-Particles

Current research deals with the appearance of localized moving structures, so-called quasi-particles, in different gas discharge systems. Examinations have shown, that a binary model as described above, either does not create those structures at all, or only in very special parameter areas. That is why the following three-component-reaction-diffusion-model is being examined at the moment.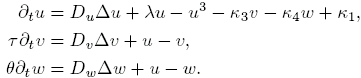

Due to this model it is possible to explain quasi-particle-solutions. The underlying mechanism is also valid for one-, two- and three-dimensional systems. The following images show quasi-particles in two- and three-dimensional systems. The "applet cellular"  (optimized for Netscape Navigator) is the implementation of a cellular automata, which realises the three-component system named above, using easy rules. It can also show moving localized resolution.

Quasi-particles in a three-component-reaction-diffusion system. The direction of motion results by a shift of the component v against the component u. These structures exist on two- and three dimensional domains.

Scattering Quasi-Particles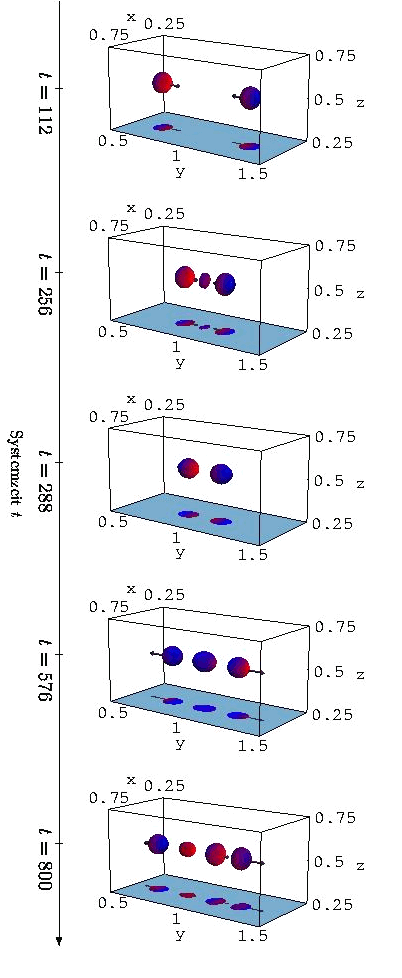

To examine the interaction of dissipative quasi-particles, the three-component-reaction-diffusion system is solved on three-dimensional domains and in time. Thatfor we will use a finite difference algorithm which will be calculated by the Cray T3E of the High-Performance Computing-Centre Stuttgart. In dependency on the system parameters, you can observe scattering, annihilation and generation (see the image on the right) of quasi-particles. Furthermore complex structures can be see that disintegrate on the other hand into quasi-particles due to symmetry breaking. Normally the tails of quasi-particles decay exponentially to the homogeneous background state, but for special parameters some oscillating behaviour is observed which leads to the formation of quasi-particle-molecules. If the amplitudes of these oszillating tails are to huge, the tails of two quasi-particles can superimpose and generate a third particle. The tails of this new particle will superimpose with the ones of his neighbours and further quasi-particles will be generated in a chain reaction like process.

Reduced Dynamics

Theoretical investigation in the parameter range D_w® 0 and q® 0 admit an analytical prediction concerning the transition from stationary to moving structures . This mechanism is based on a slowdown of the inhibitor v. This component does not react fast enough on the shifting of the component u any more, so that the displacement leads to a propagation or to a rotation, if the structure is rotational invariant like quasi-particle-molecules. It is moreover possible to calculate the interaction, namely the impacts between different quasi-particles and to compare them with simulations. Even inhomogeneities can be integrated into the model in order to predict their influence on the direction of the movement and the velocity of the movement. Here the potential annihilation or generation of particles has not been taken into consideration. One gets simple equations of movement, which can be simulated with little numeric effort. The "applet interact"  (optimized for Netscape navigator) is based on these equations of movement and admits an interactive examination of the different possibilities ]

Literature

• Dissipative Solitons in Reaction-Diffusion Systems
  Purwins, H.-G., H.U. Bödeker, A.W. Liehr
  in: N. Akhmediev, A. Ankiewicz (eds.) Dissipative Solitons
  Lectures Notes in Physics, Springer (2005)
• Rotating Bound States of Dissipative Solitons
  Liehr, A.W., A.S. Moskalenko, Yu.A. Astrov, M. Bode, H.-G. Purwins
  Eur. J. Phys. B37, 199-204 (2004)
• Measuring the Interaction Law of Dissipative Solitons
  Bödeker, H.U., A.W. Liehr, M.C. Röttger, T.D. Frank, R. Friedrich, H.-G. Purwins
  New J. Phys. 6, 62 (2004)
• Transition from Stationary to Rotating Bound States of Dissipative Solitons
  Liehr, A.W., A.S. Moskalenko, H.-G. Purwins
  In: High Performance Computing in Science and Engineering '03, Krause,E.; Jäger,W. (eds.),pp 225-234 (2003)
• Noise-Covered Drift Bifurcation of Dissipative Solitons in a Planar Gas-Discharge System
  Bödeker, H.U., M.C. Röttger, A.W. Liehr, T.D. Frank, R. Friedrich, H.-G. Purwins
  Physical Review E 67, 56220 (2003)
• Drift-Bifurcation Detection for Dissipative Solitons
  Liehr, A.W., H.U. Bödeker, M.C. Röttger, T.D. Frank, R. Friedrich, H.-G. Purwins
  New Journal of Physics 5, 89.1 - 89.9 (2003)
• Rotational Bifurcation of Localized Dissipative Solitons
  Moskalenko, A.S., A.W. Liehr, H.-G. Purwins
  Europhysics Letters 63, 361 (2003)
• Interaction of dissipative Solitons: Particle-Like Behaviour of Localized Structures in a Three-Component Reaction-Diffusion System
  Bode, M., A.W. Liehr, C.P. Schenk, H.-G. Purwins
  Physica D 161, 45 (2002)
• Pattern Formation in Dissipative Systems: A Particle Approach
  Bode, M
  In: B. Kramer (Hrsg.): Advances in Solid State Physics, Vol. 41, Springer, 2001, S. 369-381
• The Generation of Dissipative Quasi-Particles near Turing´s Bifurcation in Three-Dimensional Reaction-Diffusion Systems
  Liehr, A.W., M. Bode, H.-G. Purwins
  Projekt Dynamical Structures in Three-Component Reaction-Diffusion Systems des Höchstleistungsrechenzentrums Stuttgart (HLRS), Springer (2001)
• Dissipative Quasiteilchen in dreikomponentigen Reaktions-Diffusions-Systemen
  Liehr, Andreas W.
  Diplomarbeit, Institut für Angewandte Physik, Westfälische Wilhelms-Universität Münster, 1999
• Numerische und analytische Untersuchung solitärer Strukturen in zwei- und dreikomponentigen Reaktions-Diffusions-Systemen
  Schenk, Christian P.:
  Dissertation, Institut für Angewandte Physik, Westfälische Wilhelms-Universität M¨nster, 1999
• Spot Bifurcations in Three-Component Reaction-Diffusions Systems: The Onset of Propagation
  Or-Guil, M., M. Bode, C.P. Schenk, H.-G. Purwins
  Phys. Rev. E. 57, 6432-6437 (1998)
• Interaction of Self-Organized Quasiparticles in an Two-Dimensional Reaction-Diffusion System: The Formation of Molecules
  Schenk, C., P. Schütz, M. Bode, H.-G. Purwins
  Phys. Rev. E 57, 6480-6486 (1998)
• Interacting pulses in three-component reaction-diffusion systems on two-dimensional domains
  Schenk, C.P., M. Or-Guil, M. Bode, H.-G. Purwins
  Phys. Rev. Lett. 78, 3781-3784 (1997)
• Summary on Work on Reaction Diffusion Systems (PDF)