Institute of Applied Physics
Nonlinear Systems and Patternformation - Magnetism - Material Science - Applied Physics

Institute of Applied PhysicsNonlinear Systems and Patternformation - Magnetism - Material Science - Applied Physics |
 |
Pattern formation in planar dc gas-discharge systemsOverviewThis page gives information about the investigations performed in the work group of Prof. Purwins concerning the topic "Pattern formation in planar dc gas-discharge systems". The following topics are treated:
Why investigations on pattern formation in planar gas-discharge systems ?In modern research, the formation of complex patterns is of central interest and is therefore considered as one of the most important research topics for the next decades (see also Research perspectives of the MPG). In order to understand the universality of complex processes in nature, it is necessary to find physical systems which on the one hand exhibit a distinctive tendency to show different processes of pattern formation and which on the other hand allow for a good theoretical and experimental treatment. These claims are fulfilled by electrical transport systems which can be observed both in many examples in nature (e.g. lightnings and plasmas) as well as in technical applications (e.g. discharge tubes, plasma etching and TFT monitors). While the well known long discharge tubes already known in the 19th century represent longitudinal systems, the research group investigates planar systems with high-ohmic barrier (Fig. 1). The system differs from longitudinal discharge systems because of its small aspect ratio and the use of a high-ohmic semiconductor electrode. If a sufficiently large current is applied to the electrodes, spatially and temporally inhomogeneous patterns can form in the discharge gap (see below). The essential patterns develop in lateral direction and not in the direction of the discharge current as known from long tubes. 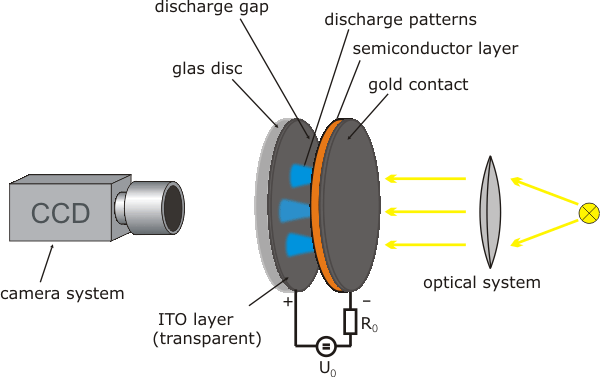
Fig. 1: Planar gas-discharge system with high-ohmic barrier (schematically) The diversity of the observable patterns in planar gas-discharge systems is much larger than in longitudinal systems. The investigations lead both to general statements about patterns-forming systems as well as to important insights concerning the nature of electrical transport systems for which up to now no standardized theory exists. Using discharge gap widths in the sub-millimeter range, the question arises if classical methods of describing gas-discharge systems, e.g. in terns of drift-diffusion models, can be applied. Sophisticated theoretical models are needed to to describe and to understand dynamical phenomena taking place on very fast to very slow time scales. Supportingly, numerical simulations of the dynamical equations have to take place on powerful computer systems. Observed patterns
Fig. 2: Examples of experimentally observed patterns The system under investigation features a large richness of structures that can be observed in the luminance density distribution of the gas-discharge. From the luminance density distribution, one may draw conclusions concerning the microscopic current density distribution in the gas as it is proportional to the luminance density distribution. Fig. 2 shows a selection of the large variety of the experimentally observed patterns. One finds stripe patterns (2.a), target patterns (2.d), spirals (2.c), labyrinth patterns (2.d) and hexagonal arrangements (2.e). Patterns that are of particular interest are bright spots (2.f) which actually are localized current filaments. They prove to be very robust with respect to fluctuations, exhibit particle-like properties and are therefore also referred to as dissipative solitons. They can be stationary but tend to propagate in most of the observed cases. Dissipative solitons do not only appear as isolated structures but also show a complex interaction behavior.They can exhibit scattering processes, the formation of "molecules" (2.g) and also more complex superstructures. For example, the formation of nets (2.h) and chains (2.i) can be observed. In particular, one may observe structures corresponding to states of aggregation, and different "phases" can be coexist one one domain (2.j). Figs. 3.a and b show the average current density distributions of isolated dissipative solitons for different system parameters. Depending on these parameters, both a monotonous (3.a) as well as an oscillatory decay (3.b) to the homogeneous ground state can be observed.
Figs. 3: a and b: Averaged current density distributions for isolated dissipative solitons, c and d: generation of a dissipative soliton Aside from numerous dynamical processes like scattering and the formation of molecules in which the shape of the dissipative solitons stays essentially preserved, there are also processes in which the structure are generated or annihilated as a whole. A typical generation process is shown in Fig. 4, a dissipative soliton is generated in a typical distance near two other dissipative solitons on a timescale of a millisecond. In order to explain the observed phenomena, the group follows different approaches (compare also Section Theoretical considerations). The system under investigation is basically an electrical transport system, so that currently a description using a drift-diffusion approximation of the transport equations is developed. In parallel, Monte-Carlo- and PIC (particle-in-cell)-simulations are planned to understand microscopic processes on a very fast time scale. Aside from this works, it is possible using a phenomenological synergetic approach to describe the system using a coupled network of equivalent circuits that can be transformed into a system of reaction-diffusion equations by making a transition to a continuous limit. Many of the experimentally observed phenomena can also be observed in other pattern-forming systems such as nonlinear optics, granular media, hydrodynamics, chemical systems and electrical transport systems. It is essential to understand the fundamental mechanisms of pattern formation in these systems in order to understand the physics of more complex systems as e.g. encountered in biology. There is hope that clarifying this subject for planar gas-discharge systems may not only lead to new insights in the area of gas-discharge physics, but also to improvements in the understanding of the universality of the observed phenomena. The following list contains some selected articles on the described phenomena: Stripe patterns
Hexagons
Spirals
Target patterns
Dissipative solitons
Experimental investigationsExperimentally controlling the planar gas-discharge system shown in Fig. 1 requires a good knowledge of different properties of the material and the corresponding techniques of preparation. A general claim is a high spatial homogeneity which must be guarantied by a careful experimental verification. The parameter space of the system is rather high-dimensional, e.g., the sort of the filling gas, the gas pressure, the semiconductor material and its resistance, the external resistivity, the temperature and the spatial dimensions of the discharge cell can be varied. As numerous patterns turn out to be more stable at lower temperatures, most of the experiments take place at cryogenic temperatures around 100 K, demanding the use of appropriate vacuum apparatus (Fig. 4).
The observation of the observed phenomena is performed via the luminance density emitted from the discharge gap, allowing to estimate the local current density. The dynamics of the discharge takes place on a number of different time scales from a nanosecond scale to a sub-second scale. Accordingly, different cameras and recording techniques are available to allow for an experimental investigation of the dynamics. The group owns usual CCD cameras with video frequency, intensified CCD cameras with larger frame rates (f = 3000 Hz) and a large memory as well as ultrafast streak cameras with very high frame rates. To process the recorded data, several powerful self-programmed applications are available. For the comparison with theoretical considerations, an investigation of the regions of existence of different patterns in the parameter space of the discharge system and a classification of the transitions between the different patterns according to the occurring types of bifurcation is of particular importance. A further central aspect is the generation and dynamics of localized patterns (Fig. 2.f) because of the numerous particle-like properties of these structures. It turns out that the dynamics and the interaction of the dissipative solitons in the experiment is superimposed by strong fluctuations. This makes it difficult to give quantitative statements about the dynamics in an elementary way. A solution for this problem is given by the application on newly developed methods of stochastic data analysis. Aside from the investigation of the actual phenomena of pattern formation, an analysis of the elementary properties of the gas-discharge in planar systems (e.g. the measurement of Paschen curves, current-voltage characteristics, the temporal evolution of currents, surface charges etc.) plays an important role, especially to establish a connection with the theoretical investigations. A good overview on the described problems is given by the following articles:
|
|
© 2011 Institute of Applied Physics |