Pattern formation in planar gas-discharge systems

Overview

This page gives information about the investigations performed in the work group of Prof. Purwins concerning the topic "Pattern formation in planar dc gas-discharge systems". The following topics are treated:

• Why pattern formation in planar gas-discharge systems ?
• Observed patterns
• Experimental investigations
• Theoretical considerations
• Numerical investigations
• Advanced data analysis

Theoretical considerations

The central goal of the theoretical investigations on planar gas-discharge systems is to make statements on the mechanisms underlying the observed phenomena of pattern formation. As numerous systems exhibiting pattern formation are fundamentally different on a microscopic level but exhibit extremely similar phenomena on a macroscopic scale, it seems obvious that a substantial understanding of the observed phenomena must take place on a meta level between microscopic and macroscopic scales.

From a microscopic point of view, the experimentally investigated system is a hybrid electrical transport system. Different charge carrier species, such as electrons and ions, as well as excited species in the gas and electrons, holes and excited states in the semiconductor play a role in the discharge. An adequate theoretical treatment requires a suitable modelling (i) of the gas-discharge, (ii) of the semiconductor and (iii) of the external electric circuit. The currently used model for the gas is based on a hydrodynamic description, the central equation is the transport equation

for the concentration of the electrons (index e) and the concentration of one ionic species (index i). The transport of the electrons and ions is characterized by a drift in the external electric field and by diffusion. The continuity equation

describes the temporal change of the charge carrier concentration, where in the simplest case of direct ionization by electron collisions the source term is given by

The Poisson equation

establishes a connection between the local electric field and the local charge carrier density by which the system gets self-consistent. For the high-ohmic electrode, one may assume in the simplest approximation that it is characterized by a constant resistivity, giving a connection between the field strength and the current density by Ohms law. In a more detailed description, the semiconductor can be described in drift-diffusion approximation. The equations for the external electric circuit can be found by applying the Kirchhoff laws. The boundary conditions on the electrodes include both Gamma processes by secondary electron emission as well as a separate equation for charges accumulated on the surfaces.

Apart from the model presented above, different authors have presented other models to describe gas-discharge systems (e.g. by using a Boltzmann equation or by modelling the particle dynamics with Monte-Carlo methods), which are able to describe many more details of the discharge. However, already the simple drift-diffusion approximation has the problem that a numerical solution of the model equations may possibly take hold of processes that occur on a millisecond time scale while the experimentally observed phenomena may take place on a time scale of seconds. Therefore a further reduction of the equations is necessary to take account of phenomena on very slow time scales.

The simplification of the equations can be done in two different ways. One possibility is to exploit the fact that in the original system, two different time scales can be found (namely the mean drift times of the electrons (in the region of nanoseconds) and of the ions (in the region of milliseconds). As the interesting processes take place on a time scale which is much slower than the ionic drift time, the equations can be averaged over many avalanche processes. If the system is e.g. in the mode of Townsend dark discharge, one may find the nonlinear reaction-diffusion equation

as an averaged equation for the axial current density. The diffusion coefficient is given by the ambipolar diffusion coefficient which corresponds to the radial diffusion of charge carriers. In the reaction term, aside from the current density one finds the variation of the voltage U as overvoltage. It can depend on the spatial coordinates, making the overvoltage a spatially dependent dynamic variable (in contrast to systems with metallic electrodes). The equation describes slow processes as long as the overvoltage is small, and is coupled to the equations for the semiconductor electrode and for the external electric circuit.

The process of reduction is technically rather complicated, especially when more than one ionization channel or a separate equation for neutral species is involved. However, the resulting equations are of the same type : reaction-diffusion equations with one or more components. The experimentally observed pattern formation phenomena are often qualitatively similar for different gases. Therefore it is natural to assume that a universal mechanism is responsible for the observed phenomena which can be described by a simple and universal model system. As an alternative to the microscopic modelling, one may also use a more synergetic phenomenological ansatz. In this approach, microscopic details are without relevance, instead, one poses the question which macroscopic properties dominate the processes of pattern formation. To this end, the spatially extended system is divided into many infinitesimally small cells. Each of the cells is assigned an electrical equivalent circuit taking account only of the most relevant macroscopic properties of the system. Consequently, a high ohmic resistivity and a capacity is assumed for the semiconductor layer while the gas layer is characterized by a nonlinear current-voltage characteristic and an inductivity (Fig. 5).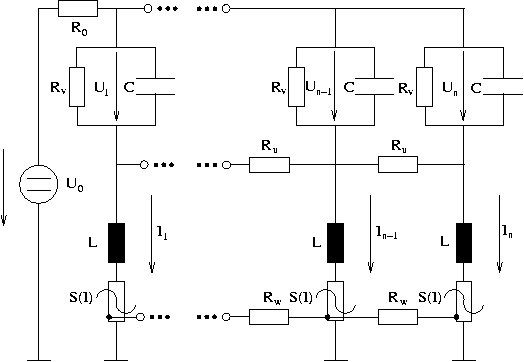

If all cells are coupled and a transition to a continuous limit is performed, one arrived at two-component reaction-diffusion systems of the form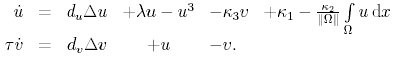

If additionally the influence of surface charges is considered, one obtains the three-component system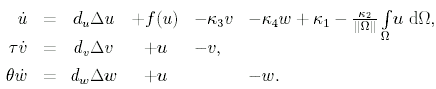

The investigation of patterns in reaction-diffusion systems is an independent topic of research . Nevertheless, a close connection to the physics of planar gas-discharge systems exists as the solutions of the reaction-diffusion equations comprise localized solutions which have strong similarities with the experimentally observed dissipative solitons (compare Section Numerical investigations). For reaction-diffusion equations, it was possible to find a drift bifurcation from stationary to propagating localized structures. This bifurcation can be described by order parameter equations which for a single dissipative soliton can be reduced to the form

near the drift bifurcation point. In addition, also the interaction between several dissipative solitons can be taken into account if the shape of the dissipative solitons does not change too significantly during the interaction process, and one obtains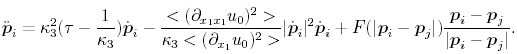

The equations allow for a comparison of the theoretical statements with experimental findings, which can take place in a quantitative way due to the fluctuations in the experimental system only by employing methods of stochastic data analysis. It is the goal of future works to investigate of how the reduced description of the order parameter equations can be used for the microscopic model equations. In this way, macroscopically observable phenomena can be directly connected to microscopic quantities.

The following articles treat the modelling of the gas-discharge system and the derivation of order parameter equations:

Microscopic modelling

• Ionization Fronts in Planar DC Discharge Systems with High-Ohmic Electrode
  Amiranashvili Sh., S. Gurevich, H.-G. Purwins
  Phys. Rev. E 71, 066404-1 (2005)

Phenomenological modelling

• Application of the Activator Inhibitor Principle to Physical Systems, H.-G. Purwins, C. Radehaus, T. Dirksmeyer, R. Dohmen, R. Schmeling, H. Willebrand, Phys. Lett. A 136 (9), 480 - 484 (1989)
• Spatiotemporal filamentary patterns in a dc-driven planar gas discharge system, C. Radehaus, H. Willebrand, R. Dohmen, F.-J. Niedernostheide, G. Bengel und H.-G. Purwins, Phys. Rev. A 45, 2546 - 2557 (1992)
• Hexagon structures in a two-dimensional dc-driven gas discharge system, H. Willebrand, M. Or-Guil, M. Schilke und H.-G. Purwins, Phys. Lett. A 177 (3), 220 - 224 (1993)
• Pattern Formation in Reaction-Diffusion Systems - Dissipative Solitons in Physical Systems, M. Bode und H.-G. Purwins, Physica D 86 (1-2), 53 - 63 (1995)
• Dissipative Solitons in Reaction-Diffusion Systems, H.-G. Purwins, H.U. Bödeker und A.W. Liehr, to appear in: N. Akhmediev, A. Ankiewicz (eds.) Dissipative Solitons, Springer, Lectures Notes in Physics (2004)

Order parameter equations

• Front-bifurcations in reaction-diffusion systems with inhomogeneous parameter distributions, M. Bode, Physica D 106 (3-4), 270 - 286 (1997)
• Interaction of dissipative solitons: particle-like behaviour of localized structures in a three-component reaction-diffusion system, M. Bode, A. W. Liehr, C. P. Schenk und H.-G. Purwins, Physica D 161 (1-2), 45 - 66 (2002)
• Rotational Bifurcation of Localized Dissipative Solitons
  Moskalenko, A.S., A.W. Liehr, H.-G. Purwins
  Europhysics Letters 63, 361 (2003)
• Rotating Bound States of Dissipative Solitons
  Liehr, A.W., A.S. Moskalenko, Yu.A. Astrov, M. Bode, H.-G. Purwins
  Eur. J. Phys. B37, 199-204 (2004)

 Back to top   To first page

Numerical investigations

Numerical simulations are an important basis for a comparison of theoretical and experimental results. On the one hand, the model equations which are nonlinear partial differential equations only allow for a limited analytical treatment, and especially the dynamics of transient processes can only be analyzed using numerical simulations. On the other hand, those patterns whose dynamics os of particular interest (namely dissipative solitons) exhibit a large aspect ratio and are generated by a destabilization of the homogeneous ground state in a subcritical bifurcation so that the dynamics cannot be explained by results already known for equations of the Ginzburg-Landau- or Kuramoto-Shivashinsky type.

The numerical treatment of reaction-diffusion equations is an independent topic of research. It turns out that the numerically found localized solutions exhibit strong similarities with the experimentally observed patterns. For example, one finds dissipative solitons with both monotonous and oscillatorily decaying tails (Figs. 7.a and b). In addition, standing and propagating dissipative solitons are observed which may interact with each other in a complex way. In principle, it is possible to reproduce all experimentally observed patterns. Figs. 6.c and d show the generation of a dissipative soliton in the vicinity of other dissipative solitons already known from the experiment (Figs. 3.c and d). In the future investigations, the numerical investigation of the phenomenological model shall help to identify the relevant mechanisms of pattern formation.

An important concern of current and future investigations is the analysis of the microscopic model equations, having the advantage that it will allow for a quantitative comparison with the experiment. The question whether the investigations will be successful will primarily be determined by the time scales over which the simulation can be performed. It is a central goal to reach a time scale in the sub-second region. Aside from general insights in the area of pattern formation, the investigations shall help to improve the understanding of the physics of weakly ionized low-pressure plasmas. The width of the discharge gap in the experimental investigations is so small that the question arises if the used model equations still hold in this situation. For example, non-local effects may play a significant role. In order to get a better understanding of these problems, Monte-Carlo- and PIC(particle-in-cell)-simulations are planned.

 Back to top   To first page

Advanced data analysis

In principle, the reduction of the phenomenologically found model equations to ordinary differential equations for the dynamics of dissipative solitons offers not only a possibility for a qualitative, but also for a quantitative comparison between theory and experiment as the dynamical behavior of single dissipative solitons can be directly compared to the predictions of ordinary differential equations. However, if the motion of isolated dissipative solitons is traced in the experiment, it turns out that the propagation cannot be described by the theoretically found equations. Partly, the structures move erratically with a permanent change of their direction of motion (Figs. 7.a and b).

As a reason for the different behavior in theory and experiment, one may name fluctuations that were not taken into consideration when modelling the dynamics using only macroscopic properties. In order to overcome this problem, methods of stochastic data analysis can be used. To this end, the experimentally observed dynamics of isolated dissipative solitons is described in terms of stochastic differential equations, so called Langevin equations:

The change of the filament velocity is given by a velocity-dependent deterministic part and a stochastic part that is the product of a matrix of noise amplitudes and normalized noise forces. Using symmetry arguments, the equation can be reduced even further. This enables a separate quantitative determination of the deterministic and the stochastic part from experimentally obtained time series of the dynamics. Generically, one finds two different states. The solitons may exhibit a damped, noise-driven propagation corresponding to Brownian motion or they may propagate with a dynamically stabilized intrinsic velocity superimposed by fluctuations (sometimes also referred to as active Brownian motion). A theoretically predicted supercritical transition between the two states with a typical scaling law can also be found (Fig. 8).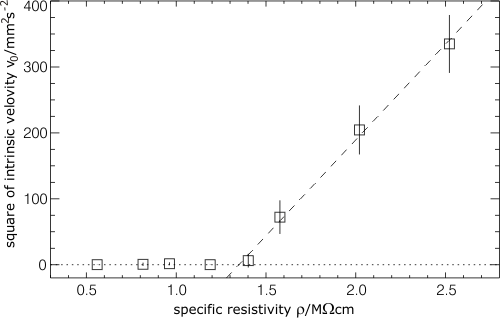

It is even possible to measure the interaction between the dissipative solitons, expanding the Langevin equations in an appropriate way:

The determination of the interaction is again done analyzing experimentally obtained time series for the dynamics, typically, one obtains a distance-dependent interaction law, its sign alternating with the distance if the dissipative solitons (Fig. 9):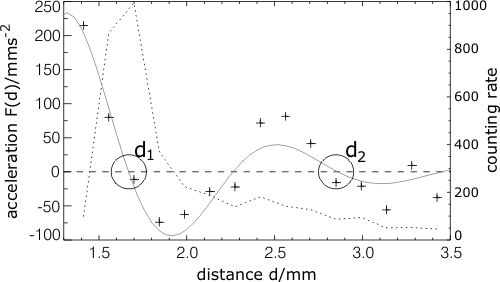

The measured interaction laws are able to quantitatively explain the observed interaction processes like scattering and the transient formation of soliton molecules. The results therefore represent an important basis for the comparison with microscopic theories. More details about methods of stochastic data analysis and their application are contained in the following articles

• Noise-influenced dynamics of dissipative solitons in a planar gas discharge system, H. U. Bödeker, M. C. Röttger, A. W. Liehr, T. D. Frank, R. Friedrich and H.-G.Purwins, Phys. Rev. E 67, 056220 (2003)
• Drift bifurcation detection for dissipative solitons, A. W. Liehr, H. U. Bödeker, M. C. Röttger, T. D. Frank, R. Friedrich and H.-G.Purwins, N. Journ. Phys. 5, 89.1--89.9 (2003)
• Drift Bifurcation of Dissipative Solitons due to a Change of Shape: Experiment and Theory, S. V. Gurevich, H. U. Bödeker, A. S. Moskalenko, A. W. Liehr and H.-G.~Purwins, accepted at Physica D (2004)
• Measuring the interaction law of dissipative solitons, H. U. Bödeker, A. W. Liehr, T. D. Frank, R. Friedrich and H.-G.Purwins, N. Journ. Phys. 6, 62.1--62.18 (2003)

In addition to methods of stochastic data analysis, other methods are investigated to make quantitative statements about the experimentally observed behavior of dissipative solitons. For example, it is possible to analyze changes in the shape of the dissipative solitons using "principal component analysis" (PCA) and to combine this technique with other data analysis techniques. In this way, generation and annihilation processes of dissipative solitons cloud be analyzed.

 Back to top   To first page