Next: Prior mixtures Up: Mixtures of Gaussian process Previous: The Bayesian model Contents

Gaussian regression

In general density estimation problems $p(y_i\vert x_i,h)$ is not restricted to a special form, provided it is non-negative and normalised [9,10]. In this paper we concentrate on Gaussian regression where the single data likelihoods are assumed to be Gaussians

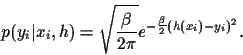$\begin{displaymath} p(y_i\vert x_i,h) = \sqrt{\frac{\beta}{2\pi}} e^{-\frac{\beta}{2} (h(x_i)-y_i)^2} . \end{displaymath}$

(6)

In that case the unknown regression function

represents the hidden variables and

-integration means functional integration $\int dh \rightarrow \int \prod_x dh(x)$ .

As simple building blocks for mixture priors we choose Gaussian (process) prior components [2,17,14],

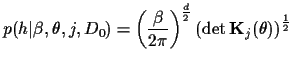		$\displaystyle p(h\vert\beta, \theta, j, D_0) = \left(\frac{\beta}{2\pi}\right)^{\frac{d}{2}} \left(\det {\bf K}_j (\theta) \right)^\frac{1}{2}$
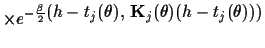		$\displaystyle \times e^{-\frac{\beta}{2} \mbox{$\left( h-t_j(\theta) ,\, {\bf K}_j(\theta ) (h-t_j(\theta)) \right)$}}$	(7)

the scalar product notation $\mbox{$\left( \cdot ,\, \cdot \right)$}$ standing for

-integration. The mean $t_j(\theta)(x)$ will in the following also be called an (adaptive) template function. Covariances ${\bf K}^{-1}_{j}/\beta$ are real, symmetric, positive (semi-)definite (for positive semidefinite covariances the null space has to be projected out). The dimension

of the

-integral becomes infinite for an infinite number of

-values (e.g. continuous

). The infinite factors appearing thus in numerator and denominator of (5) however cancel. Common smoothness priors have $t_j (\theta)=0$ and as ${\bf K}_j$ a differential operator, e.g., the negative Laplacian.

Analogously to simulated annealing it will appear to be very useful to vary the `inverse temperature' $\beta$ simultaneously in (6) (for training but not necessarily for test data) and (7). Treating $\beta$ not as a fixed variable, but including it explicitly as hidden variable, the formulae of Sect. 2 remain valid, provided the replacement $h\rightarrow (h,\beta)$ is made, e.g. $p(y_i\vert x_i,h)\rightarrow p(y_i\vert x_i,h,\beta)$ (see also Fig.1).

Typically, inverse prior covariances can be related to approximate symmetries. For example, assume we expect the regression function to be approximately invariant under a permutation of its arguments $h(x) \approx h(\sigma(x))$ with $\sigma$ denoting a permutation. Defining an operator ${\bf S}$ acting on according to ${\bf S}h(x) = h(\sigma(x))$ , we can define a prior process with inverse covariance

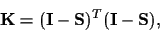$\begin{displaymath} {\bf K} = ({\bf I}-{\bf S})^T ({\bf I}-{\bf S}) , \end{displaymath}$

(8)

with identity ${\bf I}$ and the superscript ${}^T$ denoting the transpose of an operator. The corresponding prior energy

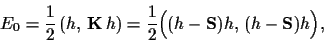$\begin{displaymath} E_0 = \frac{1}{2} \left( h, \,{\bf K}\,h\right) = \frac{1}{2} \Big( (h-{\bf S})h,\, (h-{\bf S})h\Big) , \end{displaymath}$

(9)

is a measure of the deviation of

from an exact symmetry under ${\bf S}$ . Similarly, we can consider a Lie group ${\bf S}$ = $e^{\theta{\bf s}}$ with ${\bf s}$ being the generator of the infinitesimal symmetry transformation. In that case a covariance

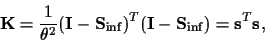$\begin{displaymath} {\bf K} = \frac{1}{\theta^2} ({\bf I}-{\bf S}_{\rm inf})^T({\bf I}-{\bf S}_{\rm inf}) = {\bf s}^T{\bf s} , \end{displaymath}$

(10)

with prior energy

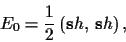$\begin{displaymath} E_0 = \frac{1}{2} \left( {\bf s}h, \,{\bf s}h\right) , \end{displaymath}$

(11)

can be used to implement approximate invariance under the infinitesimal symmetry transformation ${\bf S}_{\rm inf}$ = ${\bf I} + \theta{\bf s}$ . For appropriate boundary conditions, a negative Laplacian ${\bf K}$ can thus be interpreted as enforcing approximate invariance under infinitesimal translations, i.e., for ${\bf s}$ = $\partial/\partial x$ .

Next: Prior mixtures Up: Mixtures of Gaussian process Previous: The Bayesian model Contents

Joerg_Lemm 1999-12-21