



Next: Gaussian regression
Up: Mixtures of Gaussian process
Previous: Introduction
Contents
The Bayesian model
Let us consider
the following random variables:
- 1.
 , representing (a vector of)
independent, visible variables (`measurement situations'),
, representing (a vector of)
independent, visible variables (`measurement situations'),
- 2.
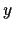 , being (a vector of)
dependent, visible variables (`measurement results'),
and
, being (a vector of)
dependent, visible variables (`measurement results'),
and
- 3.
 , being the hidden variables (`possible states of Nature').
, being the hidden variables (`possible states of Nature').
A Bayesian approach is based on two model inputs
[1,11,4,12]:
- 1.
- A likelihood model
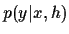 ,
describing the density of observing
,
describing the density of observing 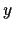 given
given  and
and  .
Regarded as function of
.
Regarded as function of  , for fixed
, for fixed 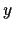 and
and  ,
the density
,
the density 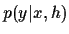 is also known as the (
is also known as the ( -conditional) likelihood of
-conditional) likelihood of  .
.
- 2.
- A prior model
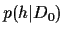 , specifying
the a priori density of
, specifying
the a priori density of  given some a priori information denoted by
given some a priori information denoted by 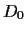 (but before training data
(but before training data 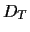 have been taken into account).
have been taken into account).
Furthermore,
to decompose a possibly complicated prior density
into simpler components,
we introduce
continuous hyperparameters 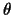 and discrete hyperparameters
and discrete hyperparameters 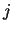 (extending the set of hidden variables to
(extending the set of hidden variables to 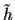 =
= 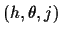 ),
),
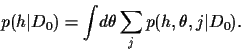 |
(1) |
In the following, the summation
over  will be treated exactly,
while the
will be treated exactly,
while the  -integral will
be approximated.
A Bayesian approach aims in calculating the predictive density
for outcomes
-integral will
be approximated.
A Bayesian approach aims in calculating the predictive density
for outcomes  in test situations
in test situations 
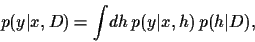 |
(2) |
given data 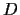 =
= 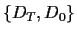 consisting of
a priori data
consisting of
a priori data 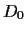 and
i.i.d. training data
and
i.i.d. training data 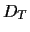 =
=
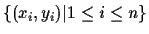 .
The vector of all
.
The vector of all 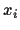 (
(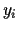 )
will be denoted
)
will be denoted 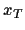
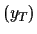 .
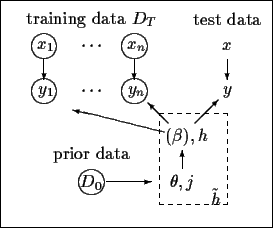
Fig.1 shows a graphical representation
of the considered probabilistic model.
.
Fig.1 shows a graphical representation
of the considered probabilistic model.
In saddle point approximation
(maximum a posteriori approximation)
the  -integral becomes
-integral becomes
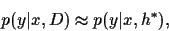 |
(3) |
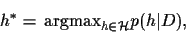 |
(4) |
assuming 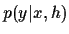 to be slowly varying at the stationary point.
The posterior density is related to
(
to be slowly varying at the stationary point.
The posterior density is related to
(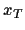 -conditional) likelihood and prior
according to Bayes' theorem
-conditional) likelihood and prior
according to Bayes' theorem
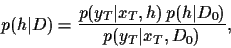 |
(5) |
where the  -independent denominator (evidence)
can be skipped when maximising with respect to
-independent denominator (evidence)
can be skipped when maximising with respect to  .
Treating the
.
Treating the 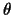 -integral within
-integral within 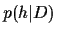 also in saddle point approximation
the posterior must be maximised
with respect to
also in saddle point approximation
the posterior must be maximised
with respect to  and
and 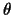 simultaneously .
simultaneously .
Figure 1:
Graphical representation of
the considered probabilistic model,
factorising according to
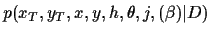 =
=
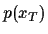
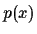
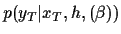
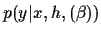
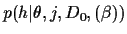
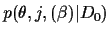 .
(The variable
.
(The variable  is introduced
in Section 3.)
Circles indicate visible variables.
is introduced
in Section 3.)
Circles indicate visible variables.
 |




Next: Gaussian regression
Up: Mixtures of Gaussian process
Previous: Introduction
Contents
Joerg_Lemm
1999-12-21
![]() and discrete hyperparameters
and discrete hyperparameters ![]() (extending the set of hidden variables to
(extending the set of hidden variables to ![]() =
= ![]() ),
),
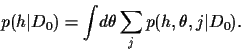
![]() -integral becomes
-integral becomes
