


Next: Maximum A Posteriori Approximation
Up: Bayesian Field Theory Nonparametric
Previous: Bayesian Field Theory Nonparametric
A Bayesian approach to empirical learning problems
requires two main inputs [1,10]:
1. a (conditional) likelihood model
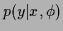 representing the probability of measuring
representing the probability of measuring 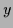 given (visible) condition
given (visible) condition 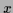 and (hidden) state of Nature
and (hidden) state of Nature  .
2. a prior model
.
2. a prior model
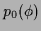 encoding the a priori information available on
encoding the a priori information available on  .
We assume that the joint probability factorizes
according to
.
We assume that the joint probability factorizes
according to
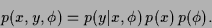 |
(1) |
Furthermore, we will consider 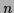 independent (training) data
independent (training) data
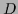 =
=
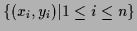 .
Denoting by
.
Denoting by
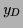 (
(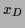 ) the vector of the
) the vector of the  (
(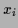 ),
we assume
),
we assume
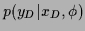 =
=
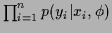 and
and
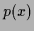 =
=
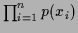 .
Different classes of likelihood functions define different problem types.
In the following we will be interested
in general density estimation problems [9],
the other problems listed in Tab. 1
being special cases thereof.
.
Different classes of likelihood functions define different problem types.
In the following we will be interested
in general density estimation problems [9],
the other problems listed in Tab. 1
being special cases thereof.
Within nonparametric approaches,
the function values 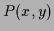 =
= 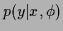 itself,
specifying a state of Nature
itself,
specifying a state of Nature  ,
are considered as the primary degrees of freedom,
their only constraint being the positivity and normalization
conditions for
,
are considered as the primary degrees of freedom,
their only constraint being the positivity and normalization
conditions for 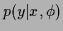 .
In particular, we will study in this paper
likelihoods
.
In particular, we will study in this paper
likelihoods 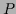 being functionals of
fields
being functionals of
fields 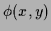 , i.e.,
, i.e., 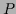 =
= 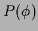 .
Examples of such functionals
.
Examples of such functionals 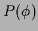 are shown in Tab. 2.
While the first and third row show
the `local' functionals
are shown in Tab. 2.
While the first and third row show
the `local' functionals 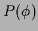 corresponding to
corresponding to
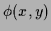 =
= 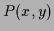 and
and
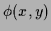 =
= 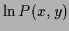 ,
the other functionals are nonlocal in
,
the other functionals are nonlocal in 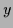 .
.
Depending on the choice of the functional 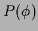 the normalization and positivity constraint for
the normalization and positivity constraint for 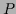 take different forms for
take different forms for  .
For example, the normalization condition is automatically fulfilled
in rows two and four of Tab. 2.
In the last row, where
.
For example, the normalization condition is automatically fulfilled
in rows two and four of Tab. 2.
In the last row, where
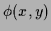 =
=
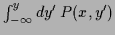 ,
the normalization constraint for
,
the normalization constraint for 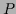 becomes the boundary condition
becomes the boundary condition
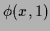 = 1, and positivity of
= 1, and positivity of 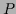 means monotony of
means monotony of 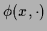 .
.
Table 1:
Special cases of density estimation.
For classification and regression see
[12,11,3,4]
and references therein,
for clustering see [8], and
for Bayesian approaches to inverse quantum mechanics,
aiming for example in the reconstruction of potentials
from observational data, see [5].
(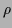 denotes the density operator of a quantum system,
denotes the density operator of a quantum system,
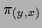 the projector to the eigenstate
of observable
the projector to the eigenstate
of observable 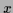 , represented by an hermitian operator,
with eigenvalue
, represented by an hermitian operator,
with eigenvalue 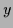 .)
.)
(conditional) likelihood 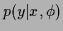 |
problem type |
| of general form |
density estimation |
discrete 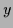 |
classification |
![$\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{[y-\phi(x)]^2}{2\sigma^2}}$](img41.png) (Gaussian,
(Gaussian, 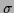 fixed) fixed) |
regression |
![$\sum_k\frac{1}{\sigma_k\sqrt{2\pi}}e^{-\frac{[y-\phi_k(x)]^2}{2\sigma_k^2}}$](img43.png) (mixture of Gaussians)
(mixture of Gaussians) |
clustering |
Trace(
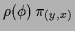 ) ) |
inverse quantum mechanics |
|
Table 2:
Constraints for some specific choices of 
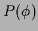 |
constraints |
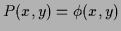 |
norm |
positivity |
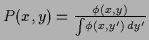 |
-- |
positivity |
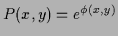 |
norm |
-- |
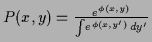 |
-- |
-- |
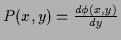 |
boundary |
monotony |
|



Next: Maximum A Posteriori Approximation
Up: Bayesian Field Theory Nonparametric
Previous: Bayesian Field Theory Nonparametric
Joerg_Lemm
2000-09-12
![]() representing the probability of measuring
representing the probability of measuring ![]() given (visible) condition
given (visible) condition ![]() and (hidden) state of Nature
and (hidden) state of Nature ![]() .
2. a prior model
.
2. a prior model
![]() encoding the a priori information available on
encoding the a priori information available on ![]() .
We assume that the joint probability factorizes
according to
.
We assume that the joint probability factorizes
according to
![]() =
= ![]() itself,
specifying a state of Nature
itself,
specifying a state of Nature ![]() ,
are considered as the primary degrees of freedom,
their only constraint being the positivity and normalization
conditions for
,
are considered as the primary degrees of freedom,
their only constraint being the positivity and normalization
conditions for ![]() .
In particular, we will study in this paper
likelihoods
.
In particular, we will study in this paper
likelihoods ![]() being functionals of
fields
being functionals of
fields ![]() , i.e.,
, i.e., ![]() =
= ![]() .
Examples of such functionals
.
Examples of such functionals ![]() are shown in Tab. 2.
While the first and third row show
the `local' functionals
are shown in Tab. 2.
While the first and third row show
the `local' functionals ![]() corresponding to
corresponding to
![]() =
= ![]() and
and
![]() =
= ![]() ,
the other functionals are nonlocal in
,
the other functionals are nonlocal in ![]() .
.
![]() the normalization and positivity constraint for
the normalization and positivity constraint for ![]() take different forms for
take different forms for ![]() .
For example, the normalization condition is automatically fulfilled
in rows two and four of Tab. 2.
In the last row, where
.
For example, the normalization condition is automatically fulfilled
in rows two and four of Tab. 2.
In the last row, where
![]() =
=
![]() ,
the normalization constraint for
,
the normalization constraint for ![]() becomes the boundary condition
becomes the boundary condition
![]() = 1, and positivity of
= 1, and positivity of ![]() means monotony of
means monotony of ![]() .
.