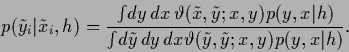Next: Predictive density
Up: Basic model and notations
Previous: Energies, free energies, and
Contents
Bayesian approaches require the calculation of posterior densities.
Model states  are commonly specified
by giving the data generating probabilities or likelihoods
are commonly specified
by giving the data generating probabilities or likelihoods 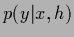 .
Posteriors are linked to likelihoods
by Bayes' theorem
.
Posteriors are linked to likelihoods
by Bayes' theorem
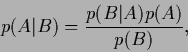 |
(14) |
which follows at once from
the definition of conditional probabilities, i.e.,
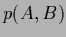 =
= 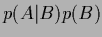 =
= 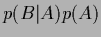 .
Thus, one finds
.
Thus, one finds
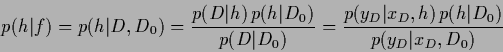 |
(15) |
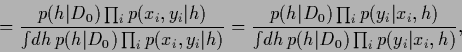 |
(16) |
using
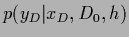 =
=
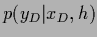 for the training data likelihood of
for the training data likelihood of  and
and
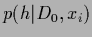 =
= 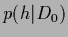 .
The terms of Eq. (15)
are in a Bayesian context often referred to as
.
The terms of Eq. (15)
are in a Bayesian context often referred to as
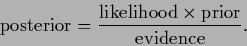 |
(17) |
Eqs.(16) show that
the posterior can be expressed equivalently
by the joint likelihoods
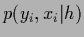 or conditional
likelihoods
or conditional
likelihoods
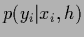 .
When working with joint likelihoods, a distinction between
.
When working with joint likelihoods, a distinction between
 and
and  variables is not necessary.
In that case
variables is not necessary.
In that case  can be included in
can be included in  and skipped from the notation.
If, however,
and skipped from the notation.
If, however, 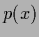 is already known or is not of interest
working with conditional likelihoods is preferable.
Eqs.(15,16) can be interpreted
as updating (or learning) formula
used to obtain a new posterior
from a given prior probability
if new data
is already known or is not of interest
working with conditional likelihoods is preferable.
Eqs.(15,16) can be interpreted
as updating (or learning) formula
used to obtain a new posterior
from a given prior probability
if new data  arrive.
arrive.
In terms of energies Eq. (16) reads,
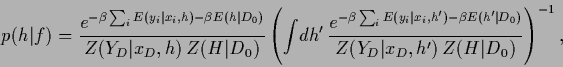 |
(18) |
where the same temperature 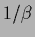 has been chosen for both energies
and the normalization constants are
has been chosen for both energies
and the normalization constants are
The predictive density we are interested in can be written as
the ratio of two correlation functions under  ,
,
where
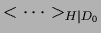 denotes the expectation
under the prior density
denotes the expectation
under the prior density
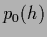 =
= 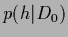 and the combined likelihood and prior energy
and the combined likelihood and prior energy 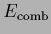 collects the
collects the  -dependent energy and free energy terms
-dependent energy and free energy terms
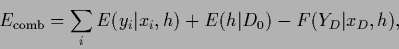 |
(24) |
with
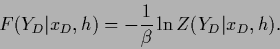 |
(25) |
Going from Eq. (22)
to Eq. (23)
the normalization factor
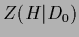 appearing in numerator and denominator
has been canceled.
appearing in numerator and denominator
has been canceled.
We remark that for continuous  and/or
and/or  the likelihood energy term
the likelihood energy term
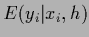 describes an ideal,
non-realistic measurement because
realistic measurements cannot be arbitrarily sharp.
Considering the function
describes an ideal,
non-realistic measurement because
realistic measurements cannot be arbitrarily sharp.
Considering the function
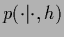 as element of a Hilbert space
its values may be written as scalar product
as element of a Hilbert space
its values may be written as scalar product
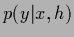 =
=
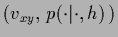 with a function
with a function 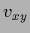 being also an element in that Hilbert space.
For continuous
being also an element in that Hilbert space.
For continuous  and/or
and/or  this notation is only formal
as
this notation is only formal
as 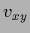 becomes unnormalizable.
In practice a measurement of
becomes unnormalizable.
In practice a measurement of
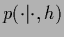 corresponds to a normalizable
corresponds to a normalizable
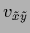 =
=
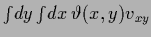 where the kernel
where the kernel
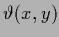 has to ensure normalizability.
(Choosing normalizable
has to ensure normalizability.
(Choosing normalizable
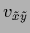 as coordinates
the Hilbert space of
as coordinates
the Hilbert space of
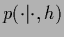 is also called a reproducing kernel Hilbert space
[183,112,113,228,144].)
The data terms then become
is also called a reproducing kernel Hilbert space
[183,112,113,228,144].)
The data terms then become
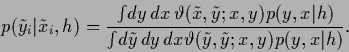 |
(26) |
The notation
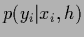 is understood as limit
is understood as limit
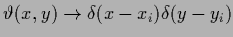 and means in practice
that
and means in practice
that
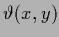 is very sharply centered.
We will assume that the discretization,
finally necessary to do numerical calculations,
will implement such an averaging.
is very sharply centered.
We will assume that the discretization,
finally necessary to do numerical calculations,
will implement such an averaging.




Next: Predictive density
Up: Basic model and notations
Previous: Energies, free energies, and
Contents
Joerg_Lemm
2001-01-21
![]() are commonly specified
by giving the data generating probabilities or likelihoods
are commonly specified
by giving the data generating probabilities or likelihoods ![]() .
Posteriors are linked to likelihoods
by Bayes' theorem
.
Posteriors are linked to likelihoods
by Bayes' theorem
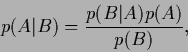
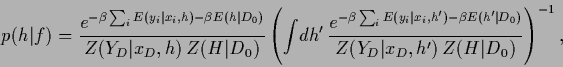
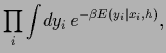
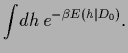
![]() ,
,
![]() and/or
and/or ![]() the likelihood energy term
the likelihood energy term
![]() describes an ideal,
non-realistic measurement because
realistic measurements cannot be arbitrarily sharp.
Considering the function
describes an ideal,
non-realistic measurement because
realistic measurements cannot be arbitrarily sharp.
Considering the function
![]() as element of a Hilbert space
its values may be written as scalar product
as element of a Hilbert space
its values may be written as scalar product
![]() =
=
![]() with a function
with a function ![]() being also an element in that Hilbert space.
For continuous
being also an element in that Hilbert space.
For continuous ![]() and/or
and/or ![]() this notation is only formal
as
this notation is only formal
as ![]() becomes unnormalizable.
In practice a measurement of
becomes unnormalizable.
In practice a measurement of
![]() corresponds to a normalizable
corresponds to a normalizable
![]() =
=
![]() where the kernel
where the kernel
![]() has to ensure normalizability.
(Choosing normalizable
has to ensure normalizability.
(Choosing normalizable
![]() as coordinates
the Hilbert space of
as coordinates
the Hilbert space of
![]() is also called a reproducing kernel Hilbert space
[183,112,113,228,144].)
The data terms then become
is also called a reproducing kernel Hilbert space
[183,112,113,228,144].)
The data terms then become