



Next: Unrestricted variation
Up: Adapting prior means
Previous: General considerations
Contents
The general case with adaptive means for Gaussian prior factors
and hyperparameter energy 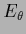 yields an error functional
yields an error functional
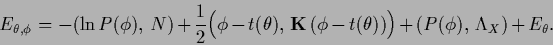 |
(432) |
Defining
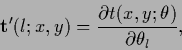 |
(433) |
the stationarity equations of (432)
obtained from the functional derivatives with
respect to  and hyperparameters
and hyperparameters 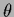 become
become
Inserting
Eq. (434) in Eq. (435) gives
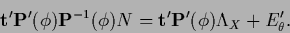 |
(436) |
Eq.(436) becomes equivalent to the parametric
stationarity equation
(356) with vanishing prior term
in the deterministic limit of vanishing prior covariances 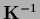 ,
i.e., under the assumption
,
i.e., under the assumption
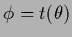 ,
and for vanishing
,
and for vanishing
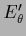 .
Furthermore, a non-vanishing prior term in (356) can be
identified with the term
.
Furthermore, a non-vanishing prior term in (356) can be
identified with the term 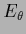 .
This shows, that parametric methods can be considered
as deterministic limits of (prior mean) hyperparameter approaches.
In particular, a parametric solution can thus
serve as reference template
.
This shows, that parametric methods can be considered
as deterministic limits of (prior mean) hyperparameter approaches.
In particular, a parametric solution can thus
serve as reference template 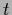 ,
to be used within a specific prior factor.
Similarly,
such a parametric solution
is a natural initial guess for a nonparametric
,
to be used within a specific prior factor.
Similarly,
such a parametric solution
is a natural initial guess for a nonparametric  when solving a stationarity equation by iteration.
when solving a stationarity equation by iteration.
If working with parameterized 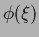 extra prior terms Gaussian in some function
extra prior terms Gaussian in some function 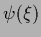 can be included
as discussed in Section 4.2.
Then, analogously to templates
can be included
as discussed in Section 4.2.
Then, analogously to templates 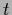 for
for  , also
parameter templates
, also
parameter templates 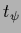 can be made adaptive
with hyperparameters
can be made adaptive
with hyperparameters 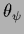 .
Furthermore, prior terms
.
Furthermore, prior terms
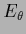 and
and
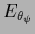 for the hyperparameters
for the hyperparameters 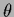 ,
, 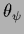 can be added.
Including such additional error terms yields
can be added.
Including such additional error terms yields
and Eqs.(434) and (434) change to
where
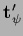 ,
,
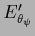 ,
,
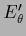 ,
denote derivatives with respect
to the parameters
,
denote derivatives with respect
to the parameters 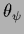 or
or 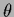 , respectively.
Parameterizing
, respectively.
Parameterizing 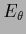 and
and
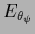 the process
of introducing hyperparameters can be iterated.
the process
of introducing hyperparameters can be iterated.




Next: Unrestricted variation
Up: Adapting prior means
Previous: General considerations
Contents
Joerg_Lemm
2001-01-21
![]() yields an error functional
yields an error functional
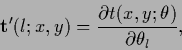
![]() extra prior terms Gaussian in some function
extra prior terms Gaussian in some function ![]() can be included
as discussed in Section 4.2.
Then, analogously to templates
can be included
as discussed in Section 4.2.
Then, analogously to templates ![]() for
for ![]() , also
parameter templates
, also
parameter templates ![]() can be made adaptive
with hyperparameters
can be made adaptive
with hyperparameters ![]() .
Furthermore, prior terms
.
Furthermore, prior terms
![]() and
and
![]() for the hyperparameters
for the hyperparameters ![]() ,
, ![]() can be added.
Including such additional error terms yields
can be added.
Including such additional error terms yields