Up to now we have formulated the learning problem
in terms of a function ![]() having a simple, e.g., pointwise, relation to
having a simple, e.g., pointwise, relation to ![]() .
Nonlocalities in the relation between
.
Nonlocalities in the relation between ![]() and
and ![]() was only due to the
normalization condition,
or, working with the distribution function,
due to an integration.
Inverse problems for quantum mechanical systems
provide examples
of more complicated, nonlocal
relations between likelihoods
was only due to the
normalization condition,
or, working with the distribution function,
due to an integration.
Inverse problems for quantum mechanical systems
provide examples
of more complicated, nonlocal
relations between likelihoods
![]() =
= ![]() and the hidden variables
and the hidden variables ![]() the theory is formulated in.
To show the flexibility of Bayesian Field Theory
we will give in the following a short introduction
to its application to inverse quantum mechanics.
A more detailed discussion of inverse quantum problems
including numerical applications
can be found in
[133,143,142,138,222].
the theory is formulated in.
To show the flexibility of Bayesian Field Theory
we will give in the following a short introduction
to its application to inverse quantum mechanics.
A more detailed discussion of inverse quantum problems
including numerical applications
can be found in
[133,143,142,138,222].
The state of a quantum mechanical systems can be
completely described by giving its density operator
![]() .
The density operator of a specific system
depends on its preparation
and its Hamiltonian,
governing the time evolution of the system.
The inverse problem of quantum mechanics
consists in the
reconstruction of
.
The density operator of a specific system
depends on its preparation
and its Hamiltonian,
governing the time evolution of the system.
The inverse problem of quantum mechanics
consists in the
reconstruction of ![]() from observational data.
Typically, one studies systems with identical preparation
but differing Hamiltonians.
Consider for example Hamiltonians of the form
from observational data.
Typically, one studies systems with identical preparation
but differing Hamiltonians.
Consider for example Hamiltonians of the form
![]() ,
consisting of a kinetic energy part
,
consisting of a kinetic energy part ![]() and a potential
and a potential ![]() .
Assuming the kinetic energy to be fixed,
the inverse problem
is that of reconstructing the potential
.
Assuming the kinetic energy to be fixed,
the inverse problem
is that of reconstructing the potential ![]() from measurements.
A local potential
from measurements.
A local potential
![]() =
=
![]() is specified by a function
is specified by a function ![]() .
Thus, for reconstructing a local potential
it is the function
.
Thus, for reconstructing a local potential
it is the function ![]() which determines the likelihood
which determines the likelihood
![]() =
=
![]() =
=
![]() =
= ![]() and it is natural to formulate the prior in terms of
the function
and it is natural to formulate the prior in terms of
the function ![]() =
= ![]() .
The possibilities of implementing prior information for
.
The possibilities of implementing prior information for ![]() are similar to those
we discuss in this paper for general density estimation problems.
It is the likelihood model where inverse quantum mechanics differs
from general density estimation.
are similar to those
we discuss in this paper for general density estimation problems.
It is the likelihood model where inverse quantum mechanics differs
from general density estimation.
Measuring quantum systems
the variable ![]() corresponds
to a hermitian operator
corresponds
to a hermitian operator ![]() .
The possible outcomes
.
The possible outcomes ![]() of measurements are given by
the eigenvalues of
of measurements are given by
the eigenvalues of ![]() ,
i.e.,
,
i.e.,
| (338) |
| (339) |
In the simplest case, where the system
is in a pure state, say the ground state ![]() of
of ![]() fulfilling
fulfilling
| (342) |
| (343) |
In contrast to ideal measurements on classical systems,
quantum measurements change the state of the system.
Thus, in case one is interested in repeated measurements
for the same ![]() ,
that density operator has to be prepared
before each measurement.
For a stationary state at finite temperature, for example,
this can be achieved by waiting until the system is again
in thermal equilibrium.
,
that density operator has to be prepared
before each measurement.
For a stationary state at finite temperature, for example,
this can be achieved by waiting until the system is again
in thermal equilibrium.
For a Maximum A Posteriori Approximation
the functional derivative of
the likelihood is needed.
Thus, for reconstructing a local potential
we have to calculate
| (344) |
| (346) |
| (347) |
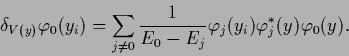 |
(348) |
| (350) |
| (351) |
The Bayesian approach to inverse quantum problems is quite flexible and can be used for many different learning scenarios and quantum systems. By adapting Eq. (349), it can deal with measurements of different observables, for example, coordinates, momenta, energies, and with other density operators, describing, for example, time-dependent states or systems at finite temperature [143].
The treatment of bound state or scattering problems for quantum many-body systems requires additional approximations. Common are, for example, mean field methods, for bound state problems [55,197,27] as well as for scattering theory [78,27,140,141,130,131,223]. Referring to such mean field methods inverse quantum problems can also be treated for many-body systems [142].