Choosing actions ![]() in specific situations
often requires the use of specific loss functions.
Such loss functions may
for example contain additional terms
measuring costs of choosing action
in specific situations
often requires the use of specific loss functions.
Such loss functions may
for example contain additional terms
measuring costs of choosing action ![]() not related to approximation of the predictive density.
Such costs can quantify aspects like
the simplicity, implementability,
production costs, sparsity,
or understandability of action
not related to approximation of the predictive density.
Such costs can quantify aspects like
the simplicity, implementability,
production costs, sparsity,
or understandability of action ![]() .
.
Furthermore, instead of approximating a whole density
it often suffices to extract some of its features,
like identifying clusters of similar ![]() -values,
finding independent components for multidimensional
-values,
finding independent components for multidimensional ![]() ,
or mapping to an approximating density with lower dimensional
,
or mapping to an approximating density with lower dimensional ![]() .
This kind of exploratory data analysis
is the Bayesian analogue to unsupervised learning methods.
Such methods are on one hand often utilized as a preprocessing step
but are, on the other hand,
also important to choose actions for situations
where specific loss functions can be defined.
.
This kind of exploratory data analysis
is the Bayesian analogue to unsupervised learning methods.
Such methods are on one hand often utilized as a preprocessing step
but are, on the other hand,
also important to choose actions for situations
where specific loss functions can be defined.
From a Bayesian point of view general loss functions require in general an explicit two-step procedure [132]: 1. Calculate (an approximation of) the predictive density, and 2. Minimize the expectation of the loss function under that (approximated) predictive density. (Empirical risk minimization, on the other hand, minimizes the empirical average of the (possibly regularized) loss function, see Section 2.5.) (For a related example see for instance [139].)
For a Bayesian version of cluster analysis, for example, partitioning
a predictive density obtained from empirical data
into several clusters,
a possible loss function is
| (64) |
For multidimensional ![]() a space of actions
a space of actions
![]() can be chosen
depending only on a (possibly adaptable) lower dimensional
projection of
can be chosen
depending only on a (possibly adaptable) lower dimensional
projection of ![]() .
.
For multidimensional ![]() with components
with components ![]() it is often useful to identify independent components.
One may look, say, for a linear mapping
it is often useful to identify independent components.
One may look, say, for a linear mapping
![]() =
= ![]() minimizing the
correlations between different components of
the `source' variables
minimizing the
correlations between different components of
the `source' variables ![]() by minimizing the loss function
by minimizing the loss function
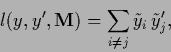 |
(65) |