 |
 |
To test the numerical implementation of
an inverse Hartree-Fock approach,
we study a two-body problem,
defined by the Hamiltonian
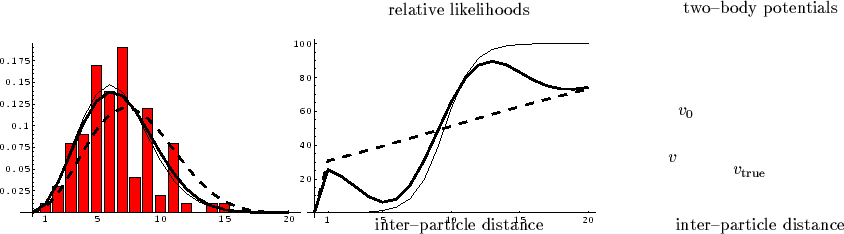
Fig. 9 shows the results of a corresponding inverse Hartree-Fock calculation. (The prior process and parameters are given in the figure caption, computational details will be presented elsewhere). For this two-body problem it is possible to calculate the exact solution and corresponding likelihood numerically. Hence, we was able to sample training data using the exact likelihood. Note that, besides the problem of simulating realistic data, an inverse Hartree-Fock calculation for more than two particles is not much more complex than for two particles. It only requires to add one single particle orbital for every additional particle. Thus, an analogous inverse Hartree-Fock calculation is clearly computationally feasible for many-body systems with three or more particles.
We have already discussed in previous sections
that, in regions where the potential is large,
the reconstruction of a potential is essentially based
on a priori information.
Training data are less important in such regions,
because finding a particle there is very unlikely.
In Fig. 9, for example,
a priori information is thus especially important for large distances.
A new, similar phenomenon occurs now when dealing with fermions:
The antisymmetry, we have to require for fermions,
forbids different particles to be at the same location.
Hence, antisymmetry
reduces the number of training data for small distances,
and a priori information
becomes especially important.
This effect can clearly be seen in the figure,
where the reconstructed potential ![]() is influenced by the data mainly for medium distances.
For large,
but also for small inter-particle distances,
the reconstructed potential
is quite similar to the reference potential.
is influenced by the data mainly for medium distances.
For large,
but also for small inter-particle distances,
the reconstructed potential
is quite similar to the reference potential.
Summarizing, we note that for inverse Hartree-Fock problems in addition to the direct Hartree-Fock Eq. (71) a second equation (81) has to be solved determining the change of Hartree-Fock orbitals under a change of the potential. Despite this complication it was possible to solve the inverse Hartree-Fock equations numerically for the example problem considered in this section.