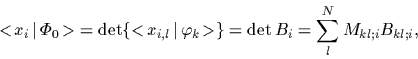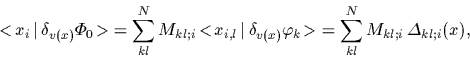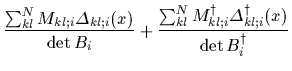Next: Numerical example of an
Up: Inverse many-body theory
Previous: Systems of Fermions
Contents
To tackle the inverse many-body problem
we will treat it in Hartree-Fock approximation
[74-77]. Thus, we replace the full many-body Hamiltonian 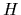 by a one-body Hartree-Fock Hamiltonian
by a one-body Hartree-Fock Hamiltonian
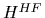 =
=
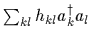 with matrix elements
with matrix elements 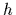 defined,
for example in coordinate representation, as
defined,
for example in coordinate representation, as
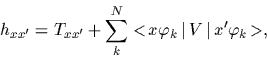 |
(70) |
the 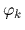 being the
being the 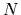 -lowest
(orthonormalized) eigenstates of
-lowest
(orthonormalized) eigenstates of 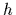 .
The corresponding
eigenvalue equation
.
The corresponding
eigenvalue equation
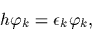 |
(71) |
is nonlinear,
due to the 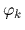 -dependent definition (70) of
-dependent definition (70) of 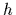 ,
and has to be solved by iteration.
The Hartree-Fock ground state
is given by the Slater determinant
,
and has to be solved by iteration.
The Hartree-Fock ground state
is given by the Slater determinant
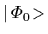 =
=
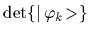 made from the
made from the 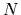 -lowest orbitals,
and has energy
-lowest orbitals,
and has energy
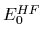 =
=
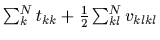 =
=
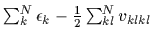 .
Considering now the case of zero temperature,
the many-body likelihood
for the true ground state
.
Considering now the case of zero temperature,
the many-body likelihood
for the true ground state 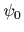 ,
,
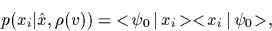 |
(72) |
becomes in Hartree-Fock approximation
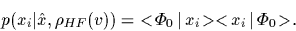 |
(73) |
The scalar product
of the Hartree-Fock ground state
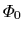 and the many-body position eigenfunction
and the many-body position eigenfunction
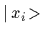 corresponding
to the measured vector
corresponding
to the measured vector 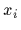 is a determinant
and can be expanded in its cofactors
is a determinant
and can be expanded in its cofactors 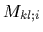
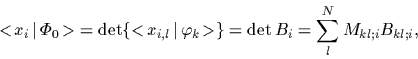 |
(74) |
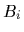 being the matrix of overlaps
with elements
being the matrix of overlaps
with elements
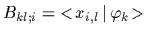 =
=
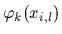 .
(For the generalization to non-hermitian
.
(For the generalization to non-hermitian  see for example
[76,78].)
see for example
[76,78].)
To maximize the posterior,
we have to calculate
the functional derivative of the Hartree-Fock likelihood
with respect to the potential
[79]
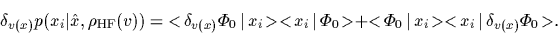 |
(75) |
Here the factors
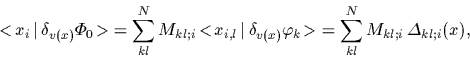 |
(76) |
can be expressed by single particle derivatives
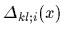 =
=
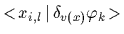 =
=
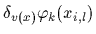 .
Analogously to Sect. 3
the functional derivatives
.
Analogously to Sect. 3
the functional derivatives
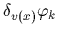 can be obtained from the functional derivative of
Eq. (71)
can be obtained from the functional derivative of
Eq. (71)
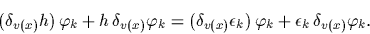 |
(77) |
Projecting onto
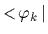 and using the hermitian conjugate of Eq. (71)
we find the Hartree-Fock version of
Eqs. (68) and (69)
and using the hermitian conjugate of Eq. (71)
we find the Hartree-Fock version of
Eqs. (68) and (69)
where we, as done before, have fixed orthonormalization and phases by
choosing
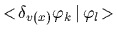 = 0
for orbitals with equal energy.
In contrast to Sect. 3, however,
= 0
for orbitals with equal energy.
In contrast to Sect. 3, however,
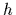 , and thus
, and thus
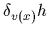 , now obey a nonlinear equation.
Indeed, from Eq. (70) it follows
, now obey a nonlinear equation.
Indeed, from Eq. (70) it follows
Inserting
Eq. (78)
and Eq. (80)
into Eq. (79),
we obtain the inverse Hartree-Fock equation
for
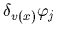
Recalling the definition of the antisymmetric matrix elements of 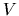 we finally arrive at
we finally arrive at
This linear equation can be solved directly
(where for Hamiltonian with real matrix elements in coordinate space
the orbitals, and thus their functional derivatives,
can be chosen real)
or, quite effectively, by iteration, starting for example with initial guess
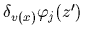 = 0.
As the
= 0.
As the
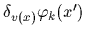 ,
which are only required for the
,
which are only required for the 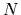 lowest orbitals,
depend on two position variables
lowest orbitals,
depend on two position variables 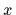 ,
, 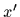 ,
Eq. (82) has essentially the dimension of a two-body equation.
Having calculated
,
Eq. (82) has essentially the dimension of a two-body equation.
Having calculated
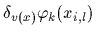 =
=
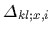 (for
(for 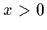 ,
, 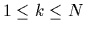 ,
, 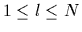 ,
, 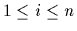 )
from Eq. (82)
the likelihood terms in the stationarity equation
(44)
follow as
)
from Eq. (82)
the likelihood terms in the stationarity equation
(44)
follow as
recalling that 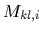 =
=
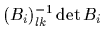 and defining
analogously to
and defining
analogously to 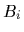 the matrix
the matrix 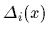 with elements
with elements
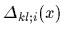 .
The freedom to linearly
rearrange orbitals within
the Slater determinants
.
The freedom to linearly
rearrange orbitals within
the Slater determinants
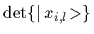 =
=
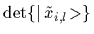 (for each data point
(for each data point 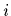 , analogously for
, analogously for
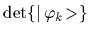 ),
makes it possible to diagonalize
the matrix of overlaps
),
makes it possible to diagonalize
the matrix of overlaps
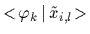 in new orbitals
in new orbitals
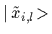 ,
which are then linear combinations of the
,
which are then linear combinations of the
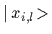 [80,78].
[80,78].




Next: Numerical example of an
Up: Inverse many-body theory
Previous: Systems of Fermions
Contents
Joerg_Lemm
2000-06-06
![]() by a one-body Hartree-Fock Hamiltonian
by a one-body Hartree-Fock Hamiltonian
![]() =
=
![]() with matrix elements
with matrix elements ![]() defined,
for example in coordinate representation, as
defined,
for example in coordinate representation, as