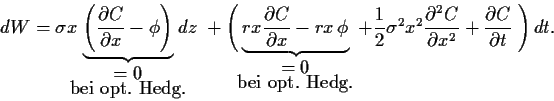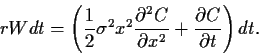Nächste Seite: Der Preis einer Call-Option
Aufwärts: Optionspreise nach Black-Scholes
Vorherige Seite: Optionspreise nach Black-Scholes
Inhalt
Wir verwenden nun den Itô-Kalkül zur Herleitung
der Black-Scholes-Formel.
Diese Herleitung findet sich beispielsweise in
[11,16,17,2,12,13].
Nehmen wir log-normalverteilte
Aktienkurse an
bei einer risikolosen Verzinsung  ,
so bedeuted dies
,
so bedeuted dies
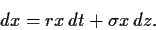 |
(55) |
Damit ergibt sich
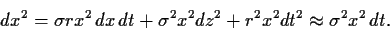 |
(56) |
Berechnen wir nun das Differential
des logarithmischen Aktienkurses ![$f[x]$](img196.gif) =
= 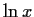 .
Mit Hilfe von Itô's Lemma (50) finden wir
für
.
Mit Hilfe von Itô's Lemma (50) finden wir
für
![\begin{displaymath}
A[x,t] = r x,
\qquad
B[x,t] = \sigma x
,
\end{displaymath}](img206.gif) |
(57) |
sowie mit
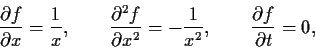 |
(58) |
daß
Also ist  normalverteilt mit
Varianz
normalverteilt mit
Varianz 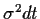 und Mittelwert
und Mittelwert
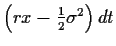 .
Daher ist die Summenvariable
.
Daher ist die Summenvariable 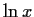 ebenfalls normalverteilt mit
Varianz
ebenfalls normalverteilt mit
Varianz 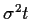 und Mittelwert
und Mittelwert
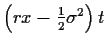 .
Wir hatten bereits gesehen, daß eine direkte Berechnung diese Resultats
ohne benutzung von Itô's Lemma
sehr viel schwieriger vonstatten ging.
.
Wir hatten bereits gesehen, daß eine direkte Berechnung diese Resultats
ohne benutzung von Itô's Lemma
sehr viel schwieriger vonstatten ging.
As nächstes betrachten wir
eine von 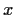 und evtl. auch von
und evtl. auch von 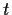 abhängige Zufallsvariable
abhängige Zufallsvariable 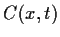 .
Solch eine Zufallsvariable wird nun im Folgenden
den Preis eines beliebigen Derivats darstellen.
Wir werden speziell den Fall
später detaillierter diskutieren
in dem
.
Solch eine Zufallsvariable wird nun im Folgenden
den Preis eines beliebigen Derivats darstellen.
Wir werden speziell den Fall
später detaillierter diskutieren
in dem 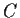 den Preis einer Call-Option represäntiert.
den Preis einer Call-Option represäntiert.
Grundlegend für den Zugang von Black-Scholes
ist die Moglichkeit durch Halten des Underlyings
des Derivats ein risikoloses Portfolio zu konstruieren.
Dazu betrachten wir ein Portfolio
bestehend aus einer Option
und von 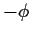 Anteilen des Underlyings,
Anteilen des Underlyings,
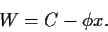 |
(60) |
Analog ist 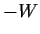 das Portfolio des Verkäufers der Option
(Schreiber, Halter der Short-Position).
Der Preis
das Portfolio des Verkäufers der Option
(Schreiber, Halter der Short-Position).
Der Preis 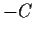 entspricht der Verpflichtung,
die der Schreiber der Option eingegangen ist.
Durch Kauf der gleichen Option, also zum Preis von
entspricht der Verpflichtung,
die der Schreiber der Option eingegangen ist.
Durch Kauf der gleichen Option, also zum Preis von 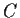 ,
kann sich der Schreiber von dieser Verpflichtung wieder
freistellen.
Die Variable
,
kann sich der Schreiber von dieser Verpflichtung wieder
freistellen.
Die Variable 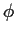 beschreibt aus dieser Sicht den
Underlyinganteil (z.B. Aktien),
den der Schreiber hält, z.B.
zum Zwecke des Absicherns der möglichen aus
dem Optiongeschäft entstehenden Verluste (hedgen).
Wir haben nun eine Kette von Zufallsvariablen definiert,
beschreibt aus dieser Sicht den
Underlyinganteil (z.B. Aktien),
den der Schreiber hält, z.B.
zum Zwecke des Absicherns der möglichen aus
dem Optiongeschäft entstehenden Verluste (hedgen).
Wir haben nun eine Kette von Zufallsvariablen definiert,
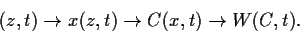 |
(61) |
Um zur Black-Scholes-Formel zu gelangen,
müssen wir nun das stochastische Differential
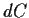 bestimmen.
Dies geschieht mit Hilfe von Itô's Lemma (50).
Zusätzlich müssen wir die Forderung nach Arbitragefreiheit
einbeziehen.
Diese wird durch eine Bedingung an
bestimmen.
Dies geschieht mit Hilfe von Itô's Lemma (50).
Zusätzlich müssen wir die Forderung nach Arbitragefreiheit
einbeziehen.
Diese wird durch eine Bedingung an 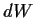 formuliert.
So gelangen wir zu einer stochastischen Differentialgleichung
für den Preis
formuliert.
So gelangen wir zu einer stochastischen Differentialgleichung
für den Preis 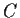 .
Als deren Lösung werden wir schließlich die
Black-Scholes-Formel finden.
.
Als deren Lösung werden wir schließlich die
Black-Scholes-Formel finden.
Nehmen an, daß während des Zeitschrittes
nicht gehandelt wird, also daß 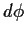 =
= 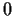 , so
gilt
, so
gilt
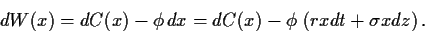 |
(62) |
Durch Anwendung von Itô's Lemma (50)
erhalten wir nun für den Preis 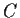 eines beliebigen Derivats,
eines beliebigen Derivats,
Damit ergibt sich
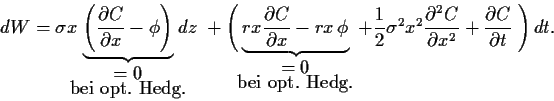 |
(64) |
Interessanterweise sieht man bereits hier, daß bei
der Wahl von
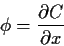 |
(65) |
der Zufallsterm 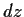 eliminiert wird
(und an dieser Stelle auch vorläufig die Variable
eliminiert wird
(und an dieser Stelle auch vorläufig die Variable 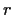 herausfällt).
Wir bezeichnen diese Wahl im Folgenden als
``optimales Hedging'',
da dadurch der Zufallseinfluß , und damit das Risiko,
vollständig eliminiert wird.
Wir erhalten damit,
herausfällt).
Wir bezeichnen diese Wahl im Folgenden als
``optimales Hedging'',
da dadurch der Zufallseinfluß , und damit das Risiko,
vollständig eliminiert wird.
Wir erhalten damit,
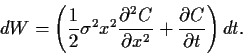 |
(66) |
Um weiterhin die Variable 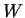 zu eliminieren,
brauchen wir eine zweite Bedingung.
Diese folgt aus der Forderung nach
Arbitragefreiheit.
In der Tat haben wir bereits diskutiert, daß Arbitragegewinne möglich sind
bei Abweichungen einer
(durch Wahl der optimalen Hedginstrategie) deterministischen
Wertentwicklung des Portfolios
zu eliminieren,
brauchen wir eine zweite Bedingung.
Diese folgt aus der Forderung nach
Arbitragefreiheit.
In der Tat haben wir bereits diskutiert, daß Arbitragegewinne möglich sind
bei Abweichungen einer
(durch Wahl der optimalen Hedginstrategie) deterministischen
Wertentwicklung des Portfolios 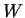 von einer sich durch
durch Verzinsung des Vermögens ergebenden
risikolosen Anlage.
Eine risikolose Verzinsung
entspricht einem Differential
[siehe Gl. (56)],
von einer sich durch
durch Verzinsung des Vermögens ergebenden
risikolosen Anlage.
Eine risikolose Verzinsung
entspricht einem Differential
[siehe Gl. (56)],
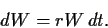 |
(67) |
Setzen wir nun also
(67)
und (68)
gleich, erhalten wir
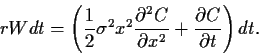 |
(68) |
Kürzen von 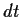 liefert,
liefert,
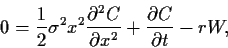 |
(69) |
und Einsetzen der Definition von 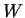 ,
,
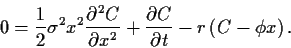 |
(70) |
Nach 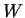 wird nun
wird nun 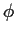 eliminiert
durch Einsetzen der optimalen Hedgingstrategie
(66),
eliminiert
durch Einsetzen der optimalen Hedgingstrategie
(66),
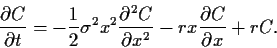 |
(71) |
Dies ist die gesuchte Differentialgleichung
von Black-Scholes.
Diese Gleichung folgt also aus:
- 1.
- Der Anwendung von Itô's Lemma
(50),
unter Annahme eines log-normal verteilten
Aktienkurses (56),
- 2.
- dem Verwenden einer optimalen Hedgingstrategie (66),
- 3.
- sowie der Annahme der Arbitragefreiheit,
entsprechend Gl. (68).
Insbesondere ist es bemerkenswert,
daß bisher keinerlei Annahmen über
die Art des Derivats, d.h. der Funktion 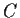 , gemacht wurden.
Die Black-Scholes Differentialgleichung
kann also verwendet werden um
den Preis beliebiger Derivate zu berechnen
(unter den notwendigen idealisierten Bedingungen,
wie fehlende Transaktionskosten, sowie der Möglichkeit
eines kontinuierlichen Handels von beliebigen Underlyinganteilen
inklusive Shortselling).
Die verschiedenen Derivate (z.B Call/Put-Optionen)
werden alleine durch die Randbedingungen unterschieden.
, gemacht wurden.
Die Black-Scholes Differentialgleichung
kann also verwendet werden um
den Preis beliebiger Derivate zu berechnen
(unter den notwendigen idealisierten Bedingungen,
wie fehlende Transaktionskosten, sowie der Möglichkeit
eines kontinuierlichen Handels von beliebigen Underlyinganteilen
inklusive Shortselling).
Die verschiedenen Derivate (z.B Call/Put-Optionen)
werden alleine durch die Randbedingungen unterschieden.
Technisch gesehen, handelt
es sich bei der Black-Scholes-Differentialgleichung
um eine Gleichung von der Art einer Diffusionsgleichung.
Die klassiche Diffusionsgleichung
 |
(72) |
enthält als Ableitungsterm in 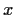 nur eine zweite Ableitung.
Zudem unterscheidet sich das Vorzeichen dieses Terms
von dem der Black-Scholes-Differentialgleichung.
Dies mag auf den ersten Blick problematisch erscheinen,
da Anfangswertprobleme für solch eine Diffusionsgleichung
mit ``falschem'' Vorzeichen
keine stabile Lösung haben.
In der Tat entspricht ein Anfangswertproblem
für solch eine Gleichung mit zusätzlichem
Minuszeichen
nach der Substitution
nur eine zweite Ableitung.
Zudem unterscheidet sich das Vorzeichen dieses Terms
von dem der Black-Scholes-Differentialgleichung.
Dies mag auf den ersten Blick problematisch erscheinen,
da Anfangswertprobleme für solch eine Diffusionsgleichung
mit ``falschem'' Vorzeichen
keine stabile Lösung haben.
In der Tat entspricht ein Anfangswertproblem
für solch eine Gleichung mit zusätzlichem
Minuszeichen
nach der Substitution
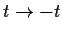 einer rückwärts zu lösenden Diffusionsgleichung,
also dem Problem bei gegeben Endzustand den entsprechenden
Anfangszustand zu suchen.
Da die Diffusionsgleichung Unebenheiten der Anfangsverteilung
glättet,
werden bei umgekehrter Zeitentwicklung
kleinste Störungen verstärkt.
Die entsprechenden Lösungen sind also nicht stabil gegenüber
kleinsten Änderungen der Anfangsverteilung.
Wie wir jetzt sehen werden, ist jedoch bei klassischen Anwendungen
der Black-Scholes-Differentialgleichung
nicht der Anfangs- sondern der Endwert von
einer rückwärts zu lösenden Diffusionsgleichung,
also dem Problem bei gegeben Endzustand den entsprechenden
Anfangszustand zu suchen.
Da die Diffusionsgleichung Unebenheiten der Anfangsverteilung
glättet,
werden bei umgekehrter Zeitentwicklung
kleinste Störungen verstärkt.
Die entsprechenden Lösungen sind also nicht stabil gegenüber
kleinsten Änderungen der Anfangsverteilung.
Wie wir jetzt sehen werden, ist jedoch bei klassischen Anwendungen
der Black-Scholes-Differentialgleichung
nicht der Anfangs- sondern der Endwert von 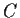 vorgegeben.
Dadurch kann Gl. (72)
durch geeignete Substitutionen
in ein Anfangswertproblem einer gewöhnlichen
Diffusionsgleichung überführt werden.
Dessen Lösungen sind stabil.
vorgegeben.
Dadurch kann Gl. (72)
durch geeignete Substitutionen
in ein Anfangswertproblem einer gewöhnlichen
Diffusionsgleichung überführt werden.
Dessen Lösungen sind stabil.




Nächste Seite: Der Preis einer Call-Option
Aufwärts: Optionspreise nach Black-Scholes
Vorherige Seite: Optionspreise nach Black-Scholes
Inhalt
Joerg_Lemm
2000-02-25
![]() ,
so bedeuted dies
,
so bedeuted dies
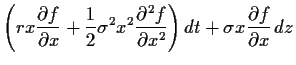
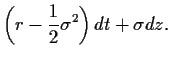
![]() und evtl. auch von
und evtl. auch von ![]() abhängige Zufallsvariable
abhängige Zufallsvariable ![]() .
Solch eine Zufallsvariable wird nun im Folgenden
den Preis eines beliebigen Derivats darstellen.
Wir werden speziell den Fall
später detaillierter diskutieren
in dem
.
Solch eine Zufallsvariable wird nun im Folgenden
den Preis eines beliebigen Derivats darstellen.
Wir werden speziell den Fall
später detaillierter diskutieren
in dem ![]() den Preis einer Call-Option represäntiert.
den Preis einer Call-Option represäntiert.
![]() Anteilen des Underlyings,
Anteilen des Underlyings,
![]() =
= ![]() , so
gilt
, so
gilt