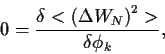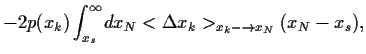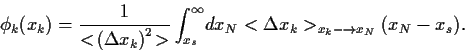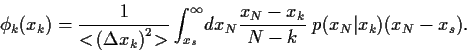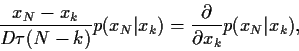Nächste Seite: Literatur
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Berechnung von
Inhalt
Nachdem wir die  -abhängigen Terme,
die zur Varianz
-abhängigen Terme,
die zur Varianz
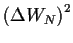 beitragen bestimmt haben, sind wir nun in der Lage
die Stationaritätsgleichung
beitragen bestimmt haben, sind wir nun in der Lage
die Stationaritätsgleichung
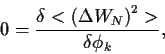 |
(87) |
(für 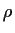 = 0)
zu lösen.
Aus Gl. (72) folgt direkt
= 0)
zu lösen.
Aus Gl. (72) folgt direkt
und damit
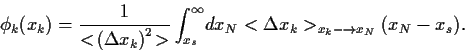 |
(89) |
Setzen wir Gl. (86), so ergibt sich,
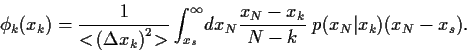 |
(90) |
Nehmen wir nun an,
daß 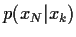 gut durch eine Gaußverteilung
in
gut durch eine Gaußverteilung
in 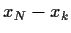 mit Varianz
mit Varianz
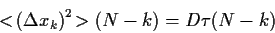 |
(91) |
approximiert wird,
so gilt
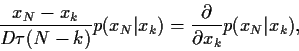 |
(92) |
und damit,
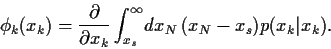 |
(93) |
Aus Vergleich mit
Gl. (42) für 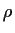 = 0
ergibt sich
die ``Delta''-Hedging Regel von
Black-Scholes,
= 0
ergibt sich
die ``Delta''-Hedging Regel von
Black-Scholes,
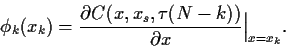 |
(94) |
Vergleich mit Abb. (9) zeigt, daß
die Ableitung des Black-Scholes-Preises
zwischen 0 und 1 schwankt.
Bei Aktienkursen weit unter dem Basispreis
ist die Wahrscheinlichkeit, daß die Option eingelöst wird
sehr gering.
Es ist deshalb für den Halter der Short-Position
nicht hilfreich selbst Underlyinganteile zu halten.
Insbesondere wäre ein Kursverlust des Underlyings nicht durch
die Short-Position einer Call-Option abgefangen.
Daher ist verständlich, daß  klein wird für kleine
klein wird für kleine 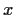 .
Bei hohen Kursen verhält sich eine Option immer mehr wie ein Forwardkontrakt.
Solch ein Kontrakt wird durch
.
Bei hohen Kursen verhält sich eine Option immer mehr wie ein Forwardkontrakt.
Solch ein Kontrakt wird durch  = 1 perfect gehedgt.
In der Tat wird dann der Verlust aus der Short-Position
exakt durch das Halten des Underlyings kompensiert.
Genau am Strikepreis ist
= 1 perfect gehedgt.
In der Tat wird dann der Verlust aus der Short-Position
exakt durch das Halten des Underlyings kompensiert.
Genau am Strikepreis ist 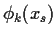 = 1/2.
= 1/2.




Nächste Seite: Literatur
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Berechnung von
Inhalt
Joerg_Lemm
2000-02-02
![]() -abhängigen Terme,
die zur Varianz
-abhängigen Terme,
die zur Varianz
![]() beitragen bestimmt haben, sind wir nun in der Lage
die Stationaritätsgleichung
beitragen bestimmt haben, sind wir nun in der Lage
die Stationaritätsgleichung