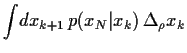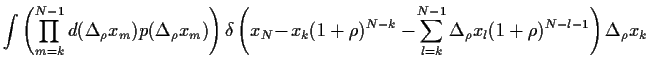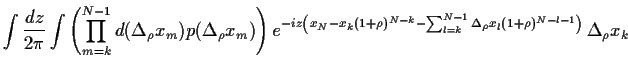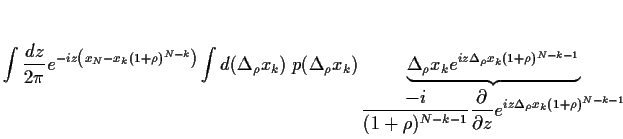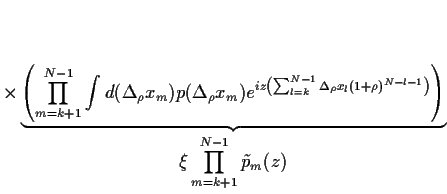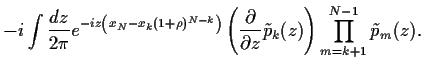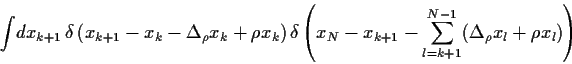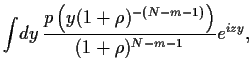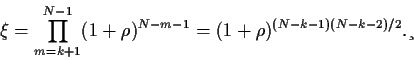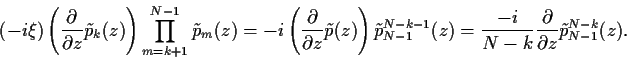Nächste Seite: Lösung der Stationaritätsgleichung
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Das Prinzip der minimalen
Inhalt
Wir berechnen nun den Mittelwert
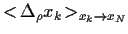 aus Gl. (80)
aus Gl. (80)
Von der zweiten zur dritten Zeile benutzten wir hierbei
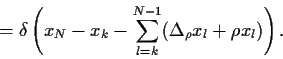 |
(82) |
Weiterhin definierten wir die Funktion
wobei 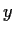 =
=
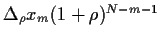 .
Für
.
Für 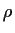 = 0 wird
= 0 wird 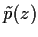 zur (unskalierten) Fouriertransformierten
zur (unskalierten) Fouriertransformierten 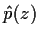 .
Aus
.
Aus 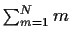 =
= 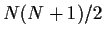 folgt
folgt
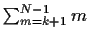 =
=
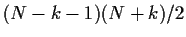 und daher
und daher
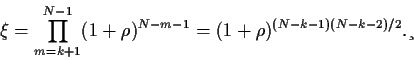 |
(84) |
Der Einfachheit halber nehmen wir im weiteren an,
daß 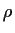 = 0.
Für identisch verteilte
= 0.
Für identisch verteilte
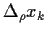 =
= 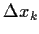 wird
wird
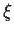 = 1,
und
= 1,
und
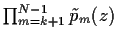 =
=
 ,
also
,
also
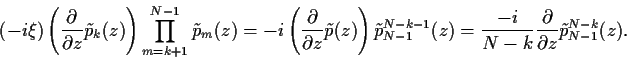 |
(85) |
Wir finden daher für 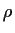 = 0
= 0
wobei wir im ersten Schritt partiell integrierten
bei verschwindenden Randtermen.




Nächste Seite: Lösung der Stationaritätsgleichung
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Das Prinzip der minimalen
Inhalt
Joerg_Lemm
2000-02-02
![]() aus Gl. (80)
aus Gl. (80)