Stability analysis

The ansatz

$$\varepsilon_i^{j+1}=g^{j}e^{ikx_i}$$

leads to the following expression for the amplification factor $g(k)$ :

$$g^2=2(1-\alpha^2)g-1+2\alpha^2g\cos(k\triangle x),$$

which after some transformations becomes just a quadratic equation for $g$ :

$$g^2-2\beta g+1=0,$$ (2.12)

where

$$\beta=1-2\alpha^2\sin^2\bigl(\frac{k\triangle x}{2}\bigr).$$

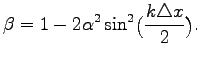
Solutions read

$$g_{1,2}=\beta\pm\sqrt{\beta^2-1}.$$

If $\beta>1$ then at least one of absolute value of $g_{1,2}$ is bigger that one. Therefor one should desire for $\beta<1$ , i.e.,

$$g_{1,2}=\beta\pm i\sqrt{\beta^2-1}$$

and

$$\vert g\vert^2=\beta^2+1-\beta^2=1.$$

In this case the scheme is conditional stable. The stability condition reads

$$-1\leq1-2\alpha^2\sin^2\biggl(\frac{k\triangle x}{2}\biggr)\leq1,%\quad \forall k\quad \Leftrightarrow\, \alpha\leq1,\\$$

what is equivalent to the standart Courant-Friedrichs-Lewy-Condition

$$\alpha=\frac{c\triangle t}{\triangle x}\leq 1.$$

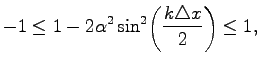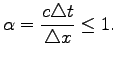
The number $\alpha$ is called the Courant number.