Distance-preserving vector space embedding for generalized median based consensus learning
Learning a consensus object from a set of given objects is a core problem in machine learning and pattern recognition. One example is text recognition, where the use of different algorithms or parameters result in different recognized texts. Consensus learning would result in one text which hopefully includes less errors than each single result.
One method to calculate this result is generlized median calculation. The generalized median of a set of objects is a new object which has the smallest sum of distances to all objects in the set. The calculation of the generalized median is often NP-Hard, for example using strings with the string edit distance. Therfore, approximative solutions are needed. Recently, prototype embedding methods were successfully used to calculate the median. Prototype embedding consists of three steps (see Figure 1):
- Embed objects into a vector space in a way that the vectors have similar distances as the objects
- Calculate the median in vector space
- Reconstruct the generalized median object from its vector representation
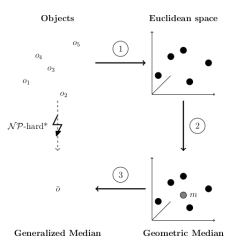
All these steps can be done easily in vector space. For the first step, prototype embedding is used, which assigns each object to a vector consisting of the objects distance to a number of selected prototype objects. While this can be done very fast, the distances of the vectors are often quite different from the distances of the objects, resulting in inaccurate median calculations. In "Distance-preserving vector space embedding for generalized median based consensus learning", we use distance preserving embedding methods to improve these results. These methods calculate embeddings which explicitly try to preserve distances of objects in vector space, resulting in better median approximations.
Another improvement of the median computation has been achieved using kernel methods. By using kernel functions instead of explicit embedding methods, one can accurately compute the relevant relationships between objects in kernel space without computing embedding vectors themselves. In our latest work we show that this leads to an even further improved median computation.
Python and Matlab Toolbox
We developed a toolbox based on this work to calculate the generlized median for any set of objects, only needing a distance function and weighted mean function between two objects which often can be derived from the distance function. Several different embedding methods are included, as well as kernel-based methods and refined reconstruction methods.
Python
A python toolbox based on this work can be found here or downloaded using pip:
$ pip install gmtb
An example file can be found here.
Matlab
Here you can download a Matlab version of the toolbox.
Included are examples using strings and the string edit distance (Levenshtein distance).
References
If you are using this work, please cite the corresponding publications:
- Nienkötter A, Jiang X. 2020. ‘Kernel-based Generalized Median Computation for Consensus Learning.’ (Submitted).
- Nienkötter A, Jiang X. 2019. ‘Distance-preserving vector space embedding for consensus learning.’ IEEE Transactions on Systems, Man, and Cybernetics: Systems.
- Nienkötter A, Jiang X. 2016. ‘Distance-preserving vector space embedding for the closest string problem.’ Contributed to the Proc. of 23rd Int. Conf. on Pattern Recognition (ICPR), Cancun, Mexico. doi: 10.1109/ICPR.2016.7899854.
- Nienkötter A, Jiang X. 2016. ‘Improved prototype embedding based generalized median computation by means of refined reconstruction methods.’ Contributed to the Proc. of Joint IAPR Int. Workshop on Structural, Syntactic, and Statistical Pattern Recognition (S+SSPR), Merida, Mexico.

