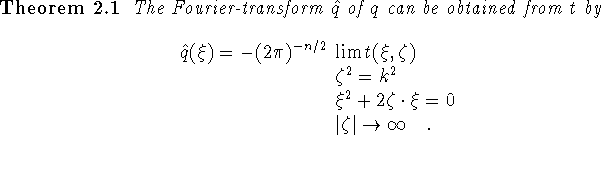This is an operator, denoted by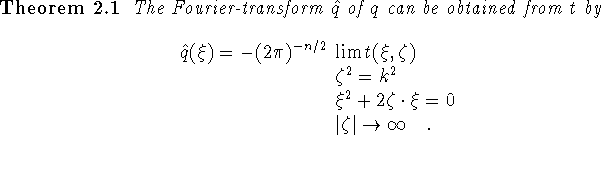 
, which acts on suitable
function spaces on 
. For a function f on
, 
is defined as follows: 
Solve (1) in 
with Dirichlet boundary values f on
and put on
.
Knowing 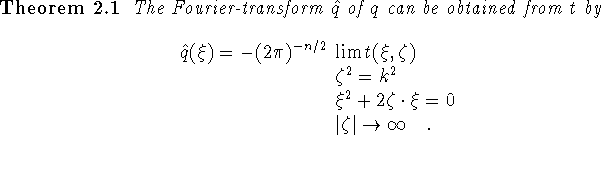we can reconstruct q. In fact, since q = 0 in
, 
satisfies
This is an exterior Helmholtz problem with a non-standard condition at
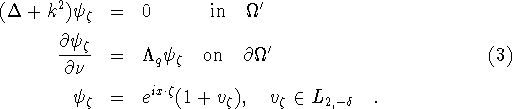and with an operator boundary condition. It can be solved,
preferably by boundary equation methods, once 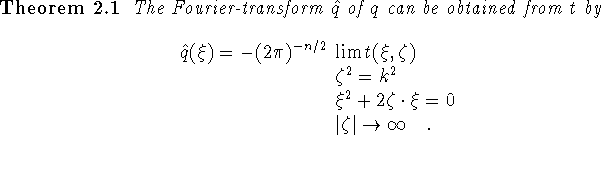is given. Then,
t can be found, whence q by Theorem 2.1.
In order to find 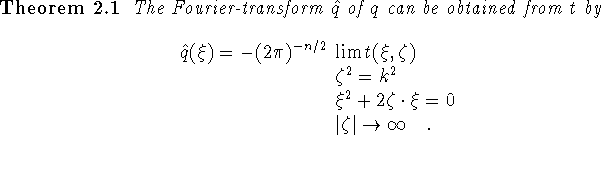from the plane-wave scattering data we
represent a function f on as
Then,
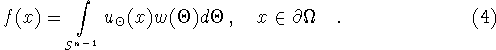
Since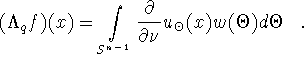 
is known for 
and 
this determines .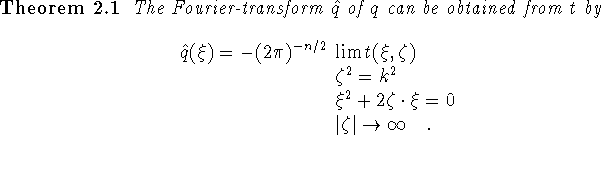
