An essential ingredient of the Nachmann - Sylvester - Uhlmann method is a
certain - non-physical - solution 
of (1) depending on the
parameter 
.
Proposition 1:
Let 
, 
and 
.
Then there is a unique solution of (1) such that
where 
and
Proof: With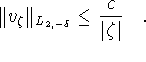 
, (1) assumes the form
In [2] it is shown that for
a sufficiently large and 
there is a constant 
such that for and
has a unique solution for each 
, and
It follows that
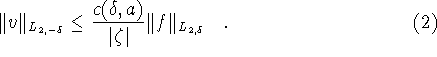satisfies
For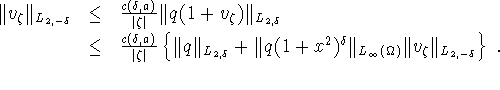 
the estimate on 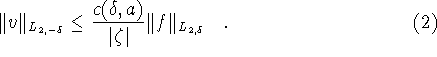follows.
The NSU method starts out from Green`s formula
With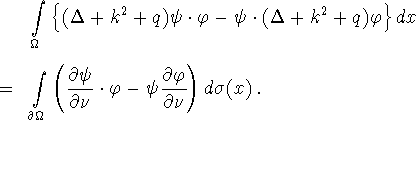 
, this reads
where
Making use of Proposition 1 we get
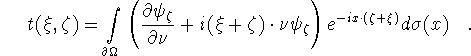
As an immediate consequence we obtain
We are left with the problem of determining t.
