We already made use of the relation
for the Radon transform in 
in section 2.1, and of the corresponding formula for the nD ray transform
in section 3.4. In this section we use these formulas to derive reconstruction algorithms. To fix ideas we consider the case of the 2D Radon transform, sampled as in the standard parallel geometry. This means that g = Rf is given for 
, 
, 
and 
, 
, as in
section 2.1. f is assumed to vanish outside 
.
The idea of Fourier reconstruction is very simple: Do a 1D Fourier transform on g with respect to the second variable for each 
. According to (6.1) this yields 
in all of 
. Do a 2D inverse Fourier
transform to obtain f. Even though this seems fairly obvious, the
numerical implementation in a discrete setting is quite intricate. In fact good
Fourier algorithms have been found only quite recently.
To begin with we describe the simplest possible implementation. We warn the reader that this algorithm is quite useless since it is not sufficiently accurate.
Algorithm 6 (Standard Fourier reconstruction.)
, ,
g the 2D Radon transform of f.
carry out
the discrete Fourier transform
, |k| < q, find j, r such
that 
is as close as possible to k and put
is an approximation to 
.
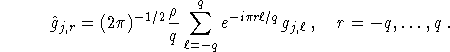
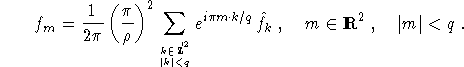
The algorithm is designed to reconstruct a function f with support in which is essentially 
-band-limited. (2.6), (2.7)
have to be satisfied. We stress again that the algorithm as it stands is not to be recommended because of poor accuracy. Better versions are described below.
A few comments are in order. In step 1 we compute an approximation 
to
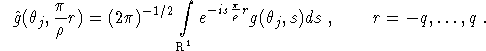
Under the assumption (2.6) this approximation is reliable since Fourier transforms are evaluated exactly by the trapezoidal rule if the Nyquist condition, in our case (2.6), is satisfied. According to (6.1), step 1 provides us with the values
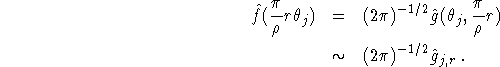
In step 2 we compute on the cartesian grid 
by nearest neighbour interpolation:
Since f vanishes outside , has bandwidth 
. Thus
sampling of on a 2D grid with stepsize 
is adequate
by the sampling theorem.
Step 3 is the trapezoidal rule for the 2D inverse Fourier transform,
properly discretized and complying with the Nyquist condition. Hence is an approximation to .
Step 1 and step 3 of Algorithm 6 are justified by the sampling theorem. Thus the failure of the algorithm must be caused by the interpolation in step 2. This is in fact the case. Of course we can replace the interpolation by a more accurate one, such as linear interpolation. However this doesn't help much.
Inspite of its poor accuracy, Fourier reconstruction is attractive because of its favourable complexity which is due to the fast Fourier transform (FFT).
We have used FFT in the circular harmonic algorithm already, but FFT is so essential for Fourier reconstruction that we say a few words about FFT; for a thourough treatment we refer to Nussbaumer (1982). The discrete Fourier transform of length q is defined to be
An algorithm which computes 
from 
in less then O 
, typically O 
, operations is a called an FFT. In the circular harmonic algorithm we have used FFT just for the evaluation of (6.3). In Fourier reconstruction
we employ FFT for the evaluation of Fourier integrals
for the functions f in 
with support in 
. Sampling theory tells us
that has to be discretized with stepsize ( has bandwidth ). With 
the stepsize for f the trapezoidal rule provides the approximation
The range of k is in agreement with the sampling theorem: The stepsize 
corresponds to the bandwidth 
, hence 
in (6.4) suffices. Of course (6.4) is a discrete Fourier transform
of length 2q. Sometimes one wants to adjust the stepsizes of f and
differently. Then one has to evaluate
with an arbitrary real parameter c. This can be done by the chirp-z-algorithm, see
Nussbaumer (1982), again with typically O operations.
Assuming that we have a fast Fourier transform (FFT) algorithm which does a discrete Fourier transform of length q with O operations, the complexity of Algorithm 6 is as follows. Step 1 does
p Fourier transforms of length 2q, requiring O 
operations. Assuming that the interpolation in step 2 can be done in O(1) operations per
point we get O as the complexity of step 2. The 2D Fourier transform in
step 3 can be done with O 
operations. Hence the complexity of
Algorithm 6 is O 
. This is much better than the filtered backprojection algorithm (Algorithm 1), which needs O 
operations for a
reconstruction on a 
grid.
Presently there exist two Fourier methods with satisfactory accuracy and favourable complexity.
1. The linogram algorithm (Edholm and Herman (1987)).
Here, interpolation in Fourier space is avoided altogether by a clever choice of the
directions 
. The linogram algorithm works on the data
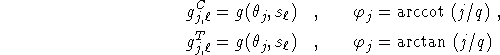
where j, . Doing a 1D Fourier transform on 
results in
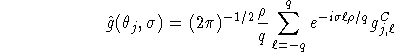
where 
arccot (j/q). For 
we get from
(6.1)
Note that this can be done efficiently by the chirp-z-algorithm. The key observation is that the points
form a grid lying on vertical lines with distance 
, being evenly spaced within
each vertical line (though with different stepsizes in different lines). On such a grid
we can do a 1D FFT in the horizontal direction in the usual way. In the horizontal
direction the stepsize is not what we need for a direct application of the FFT, but
the chirp-z-algorithm is still applicable. This takes care of the 2D inverse Fourier transform in 
. For 
we proceed analogously
with the data 
, evaluating 
for 
. We remark that the linogram data in Edholm and Herman (1987) is a little different from
ours, namely 
, 
, respectively.
The use of these detector positions makes the linogram algorithm even simpler in that the
factor 
in the right hand side of (6.6) dissapears.
2. The gridding algorithm (O'Sullivan (1985), Kaveh (1987), Schomberg and Timmer (1995).
This algorithm works on the standard parallel data which we used in Algorithm 6. It does the interpolation in step 2 of Algorithm 6 in the following way. Let w be a smooth function in with w = 1 on
which is decaying exponentially at infinity. Put 
. Then,
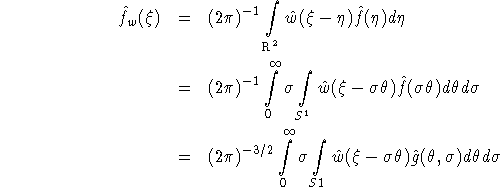
by (6.1). Using a quadrature rule with nodes 
, 
and weights 
we obtain the approximation
to 
. The method relies on the following assumptions:
is decaying at infinity so fast that only a few terms of
the r sum in (6.7) have to be retained.
If these conditions are met then 
of (6.3) is a good approximation to which can be evaluated essentially in O(1) operations for each k. This takes care of step 2. Of course when using (6.7) we have to divide f by w after step 3 to make up for the previous multiplication with w.
It is needless to say that our derivation of the gridding algorithm is purely heuristic. It seems that presently there exists no convincing theoretical analysis of the gridding algorithm.
