Parallel geometry in the plane

In this case the 2D Radon transform is sampled for , , and , . Here is the radius of the reconstruction region, i.e. we assume f(x) = 0 for , . This means that the measured rays come in p parallel bundles with directions evenly distributed over , each bundle consisting of 2q+1 equispaced lines. This was the scanning geometry of the first commercial scanner for which Hounsfield received the Nobel prize in 1979. This geometry has been replaced by more efficient ones in present day's scanners (see below), but it is still used in scientific and technical imaging.

We evaluate the integral in (2.2) by the trapezoidal rule:

 

The accuracy of this approximation can be assessed by sampling theory, according to which the trapezoidal rule for an inner product is exact provided the stepsize h satisfies the Nyquist criterion, i.e. where is the bandwidth of the factors in the inner product. In our case the first factor is (as a function of s) which has bandwidth . The second factor is (again as a function of s). This is our data and does not, in general, have finite bandwidth. At this point we have to make an assumption.

We assume f to be essentially band-limited with essential bandwidth . The nD Fourier transform of f and the 1D Fourier transform Rf (with respect to the second variable) are interrelated by

 

This is the famous (and easy to prove) ``projection'' or ``central slice'' theorem of computerized tomography. In the present context we need it only to deduce that f and g = Rf have the same (essential) bandwidth. Thus the s-integral in (2.2) is accurately represented by the -sum in (2.4) provided that the stepsize in that sum satisfies the Nyquist criterion . In other words,

 

The condition for the number p of directions which makes the j-sum in (2.4) a good approximation for the -integral in (2.2) is less obvious. Based on Debye's asymptotic relation for the Bessel functions one can show that the essential bandwidth of Rf as a function of , , is , see Natterer (1986). The stepsize h for the -integral being the Nyquist criterion requires , i.e.

 

(2.6), (2.7) are the conditions for a good accuracy in (2.4), assuming f to be zero outside the ball of radius and essentially band-limited with bandwidth .

The double sum in (2.4) has to be evaluated for each reconstruction point x. This leads to an unbearable complexity. This complexity can be reduced by introducing the function

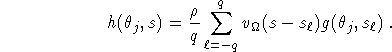
Then, (2.4) reads

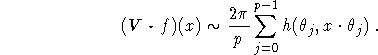
This requires only a simple sum for each reconstruction point x, at the expense of an additional interpolation in the second argument of h. In most cases linear interpolation suffices (but nearest neighbour does not!). This leads us to the filtered backprojection algorithm.

Algorithm 1 (Filtered backprojection algorithm for standard parallel geometry.)

Data:

The values , , ,

g is the 2D Radon transform of f.

Step 1:

For carry out the discrete convolution

Step 2:

For each reconstruction point x, compute the discrete

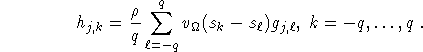
backprojection

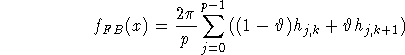
where k = k(j,x) and are determined by

Result:

is an approximation to f(x).

The algorithm depends on the parameters p, q and on the choice of . It is designed to reconstruct a function f with support in and with essential bandwidth i.e. the spatial resolution of the algorithm is . The conditions (2.6), (2.7) should be satisfied. A few remarks are in order.

1.

The condition (2.6) has to be strictly satisfied. Otherwise the s integral in (2.2) is not even approximately equal to the sum in (2.4), leading to unacceptable errors.

2.

If (2.7) is not satisfied, the reconstruction is still accurate for .

3.

Filter functions whose ``kernel sum''

does not vanish should not be used, see Natterer and Faridani (1990).

4.

Usually linear interpolation in step 2 is sufficient. However, for difficult functions f - e.g. functions containing large objects at the boundary of the reconstruction region - linear interpolation generates visible artefacts. In that case an oversampling procedure similar to the one of Algorithm 2 below is advisable. Alternatively one may use the circular harmonic algorithm from section 5.

5.

The algorithm needs O(p) operations for each reconstruction point. Algorithms with lower complexity (such as O ) can be obtained either by Fourier reconstruction, see section 6, or by the fast backprojection algorithm in section 2.5.

6.

The conditions (2.6), (2.7) suggest to take . This much debated condition is usually not complied with in radiological applications, where p is chosen considerably smaller. This is due to the special requirements in radiological imaging.