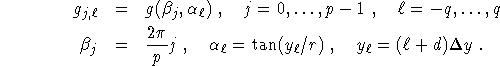
Here, the detector positions within a fan with vertex b are evenly spaced on the line perpendicular to b. We need the explicit form of the inversion formula mainly for the derivation of the FDK algorithm in 3D cone beam tomography in the next section. With g the function in (2.8), the sampled data is
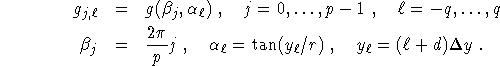
The coordinates ![]() , y are related to the parallel coordinates
, y are related to the parallel coordinates ![]() , s
in the representation
, s
in the representation ![]() of the rays by
of the rays by
Hence,
![]()
Substituting ![]() , y for
, y for ![]() , s in (2.2) leads to
, s in (2.2) leads to
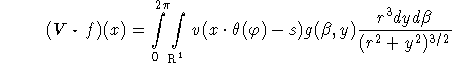
where (2.12) has to be inserted for ![]() , s. As in the standard fan beam
case a direct implementation of this formula results in an algorithm whose complexity is not competitive. Again we can circumvent this problem by exploiting the homogeneity properties
of v. A lengthy but elementary computation shows that
, s. As in the standard fan beam
case a direct implementation of this formula results in an algorithm whose complexity is not competitive. Again we can circumvent this problem by exploiting the homogeneity properties
of v. A lengthy but elementary computation shows that
![]()
![]()
From (2.11) it follows that
![]()
yielding
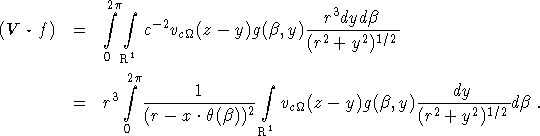
As in the standard fan beam case we make the approximation ![]() . Again this is
justified if
. Again this is
justified if ![]() , e.g.
, e.g. ![]() . Then,
. Then,
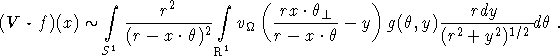
where ![]() . Defining
. Defining
this can be written as
The implementation of (2.13), (2.14) can now be done exactly as in the standard case, leading to a filtered backprojection algorithm which needs O(p) operations for each reconstruction point x.