Standard fan beam geometry

This is the most widely used scanning geometry. It is generated by a source moving on a concentric circle of radius around the reconstruction region , with opposite detectors being read out in small time intervals (third generation scanner). Equivalently we may have a fixed detector ring with only the source moving around (fourth generation scanner). Denoting the angular position of the source by and the angle between a measured ray and the central ray by ( if the ray, viewed from the source, is left of the central ray), then fan beam scanning amounts to sampling the function

 

at the points , , , , . Here, q is chosen so as to cover the whole reconstruction region with rays. d is the detector offset which is either 0 or .

First we derive the fan beam analogue of (2.1). We only have to put , to map fan beam coordinates to parallel coordinates as used in (2.1). The region of the - -plane is mapped in a one-to-one fasion onto the domain in the -s-plane, and we have

Thus (2.2) in the new coordinates reads

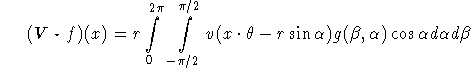
with as in (2.8). Discretizing the integral by the trapezoidal rule yields

 

This is the fan beam analogue of (2.4) and defines a reconstruction algorithm for fan beam data. One can show that for this algorithm to have resolution one has to satisfy

 

see Natterer (1993).

As in the parallel case, an algorithm based on (2.9) needs O(pq) operations for each reconstruction point. Reducing this to O(p) is possible here, too, but this is not as obvious as in the parallel case. We first establish a relation for the expression in (2.2). Let be the source position, and let be the angle between x-b and -b. We take positive if x, viewed from the source b, lies to the left of the central ray, i.e. we have

where . Let y be the orthogonal projection of x onto the ray with fan beam coordinates , . Then, . Considering the rectangular triangle xyb we see that , hence

Our filters possess the homogeneity property

 

Thus,

Using this in (2.2) we obtain

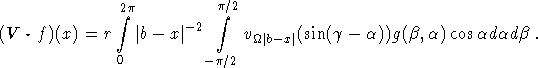
Here, , and is independent of . Unfortunately, the integral has to be evaluated for each x since the subscript depends on x. In order to avoid this we make an approximation: We replace by . This is not critical as long as , i.e. as long as . Fortunately, in most scanners , and this is sufficient for the approximation to be satisfactory. However, if is only slightly smaller than r, problems arise.

Upon the replacement of by we obtain

The integral can now be precomputed as a function of and , yielding an algorithm with the structure of a filtered backprojection algorithm.

Algorithm 3 (Filtered backprojection algorithm for parallel standard fan beam geometry.)

Data:

The values , , .

g is the function in (2.8).

Step 1:

For carry out the discrete convolutions

Step 2:

For each reconstruction point x, compute the discrete weighted backprojection

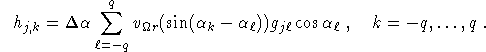
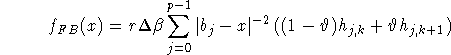
where k = k(j,x) and are determined by

the sign being the one of and ,

Result:

is an approximation to f(x).

The algorithm as it stands is disigned to reconstruct a function f with support in which essentially band-limited with bandwidth from fan beam data with the source on a circle of radius . The remarks following Algorithm 1 apply by analogy. In particular the conditions (2.10) have to be satisfied. For and with dense parts of the object close to the boundary of the reconstruction region, problems are likely to occur.