You pull a piece of paper out of your pocket with the result written on it: 6174.
Answer: 2.71828… = e, Euler's number
Question: Are there irrational numbers a and b for which the power ab is rational?
Amazingly, there is an elementary proof that such numbers exist:
Curiously, there was doubt for a while: in 1853, William Shanks published the result of his years-long calculation of 607 decimal places of π, which he later expanded to 707 places. Augustus De Morgan noticed that among the 607 digits, the number 7 only appears 44 times. The deviation from the most likely number 61 is significantly larger than one would statistically expect, and the suspicion arose that the numbers are not evenly distributed.
It was only in 1946 that D. Ferguson discovered that Shanks had made a mistake and only the first 527 digits were correct. As things stand today, π seems to be "normal".
By the way, if it is so, every finite sequence of digits would appear somewhere in it; e.g. the sequence 31415926 occurs first at the 50366472nd place after the decimal point. You can search for your birthday or other sequences on the Pi-Search Page.
The optimal strategy goes like this: You look at the proportion x (0 < x <1) of the houses. Then choose the first house that you like better than all the previous ones.
The strategy is optimal for the choice
x = 1/e ~ 0.37
Of course there is no guarantee that you will get the best house for you; if you are unlucky it could even be the worst, but for x = 1/e you are most likely to get the best house for you.
Popular is 22/7 = 3.1428... Noteworthy is the fraction 355/113 = 3.14159292..., which was discovered by the Chinese mathematician Zu Chongzhi in the 5th century, and which is easy to remember (113355). This approximation is very efficient, because it represents 7 digits of π (including the 3) using 6 digits. Are there any more efficient rational approximations?
As a measure of efficiency, let's consider the number of correct digits divided by the number of digits required. Mathematically formulated a bit better is the ratio R = - log(|π - p/q|) / log(pq).
For 22/7, R = 1.325, and for 355/113, R = 1.428.
Can it get any more efficient?
The best rational approximations for irrational numbers are provided by regular continued fractions. For π it is
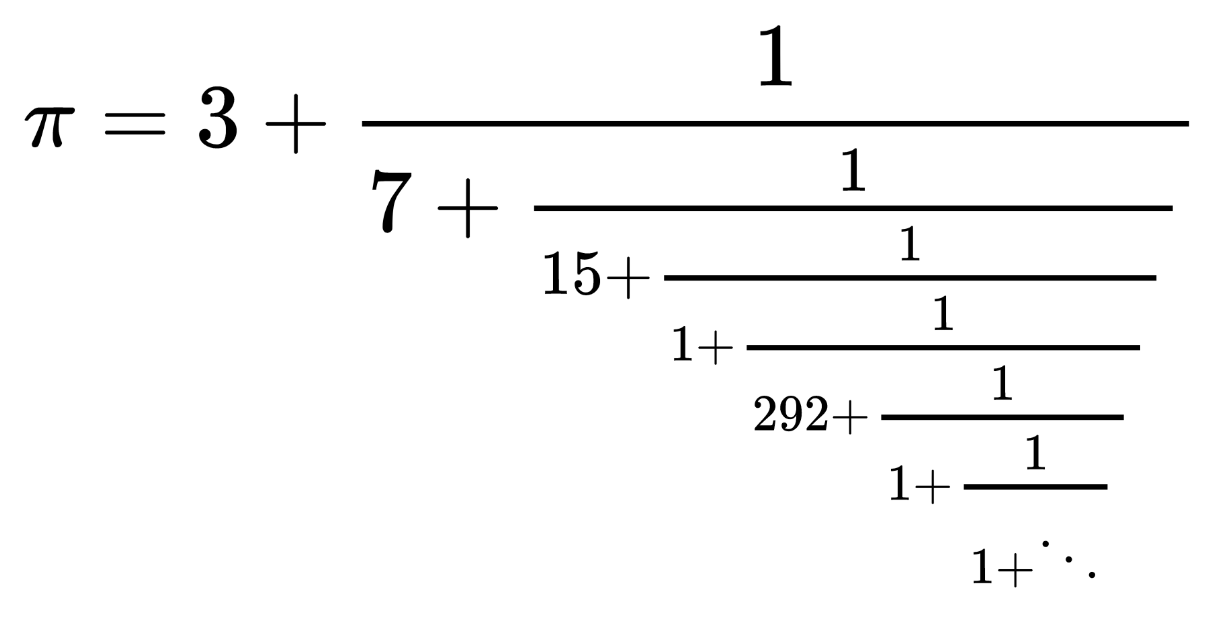
or in short notation [3;7,15,1,292,1,1,1,2,...]. Terminating the continued fraction gives the fractions 3/1, 22/7, 333/106, 355/113, ... So the fraction 355/113 appears as [3;7,15,1].
The approximation is particularly good if the continued fraction is terminated before a large denominator, here 292. If you go far enough, there are arbitrarily large denominators. The next one larger than 292 occurs after 307 steps and is 436. The corresponding p and q have 154 digits, the error to π is in the 311th digit, and the efficiency is only R = 1.007. There is probably no rational approximation more efficient than 355/113, although I know of no proof.
This led him to two hypotheses:
I. The "gravitational constant" is not constant, but decreases inversely proportional to the age of the universe.
II. The total mass in the universe grows proportionally to the square of time.
Pascual Jordan took up these hypotheses and proposed modifications of Einstein's general theory of relativity that fit Dirac's hypotheses. He also postulated that the Earth has expanded over the course of Earth's history due to decreasing gravity.
Anecdote 1: When Wolfgang Pauli heard of Jordan's theory that the mass of the universe increases quadratically with time, he commented on it with regard to Jordan's ever-increasing corpulence with the remark that it was pure anthropomorphism: Jordan was projecting his own development onto space .
Anecdote 2: In the 1950s, the physicist and philosopher Carl Friedrich von Weizsäcker proposed a theory of the universe that is based on so-called quantum theoretical "ur-alternatives". An alternative is a yes-no question. In a lecture he stated that the state of the universe is determined by a finite number of ur-alternatives, and estimated that the number of corresponding yes-no questions is given by the cube of Dirac's large number and is about 10120. Harry Lehmann (my graduate father), who was present and knew Weizsäcker from their time in Göttingen, shouted "minus one". In response to Weizsäcker's astonished question, "What do you mean, Mr. Lehmann?", he replied "10120 minus 1. One question has already been decided: I think your theory is wrong."
Addendum: Dirac's hypotheses are now considered refuted.
The key lies in the Riemann zeta function:
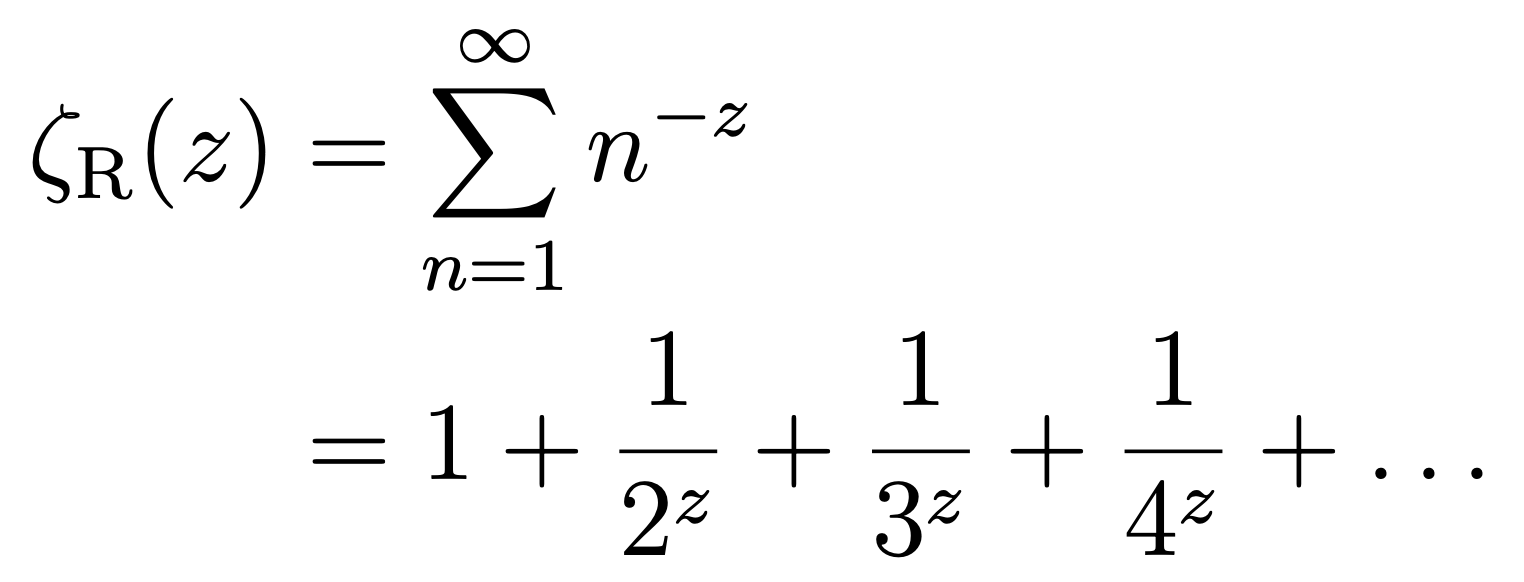
Here the variable z is a complex number. For example, for z=2 you get the sum of the inverse square numbers that Euler calculated:
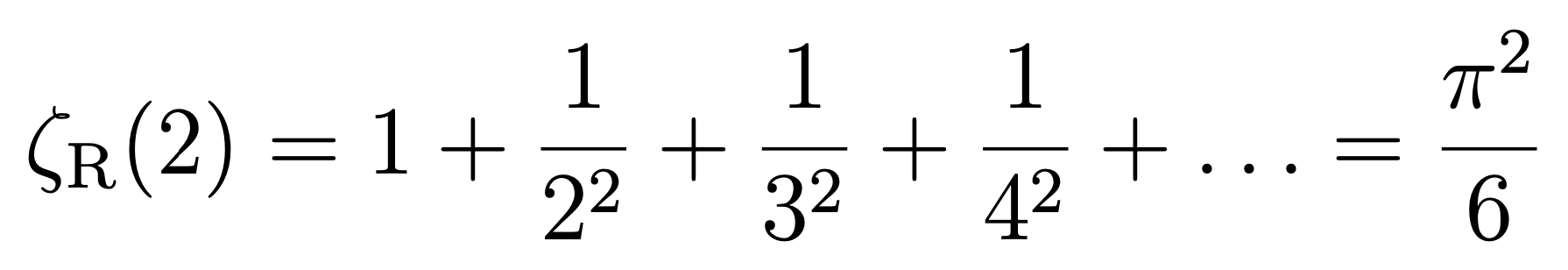
For z = -1 one would get the desired sum of the natural numbers; however, the series does not converge there. The trick is that the zeta function can be continued analytically to the entire complex plane, except for one pole at z = 1. And at z = -1 you find the value -1/12. This value of the zeta function is what actually occurs in string theory.
By the way, the "sum of squares" (z = -2) is zero.
If you are interested in details, you can find a sketch of the derivation in an article by John Baez.
A special transcendental number is the Champernowne number Q = 0.123456789101112131415... One recognizes the obvious law of formation of the decimal places. Q is even "normal" or a "number universe". This means that every finite sequence of natural numbers occurs somewhere in the decimal places of Q. In 1933, David Champernowne delivered the first explicitly constructed normal number, Q.
Your credit card pin, your IBAN, your tax number appear somewhere in the digits of Q. Now imagine there was a video with your entire life story, including the events that were to come. Stored on a very large hard drive, it is represented by a very very long string of zeros and ones. In this form, the video occurs somewhere in the distant depths of the digits of Q. So Q contains information about your entire life. Unfortunately, that doesn't help you, because Q also contains all sorts of false life stories.
Almost 80 years ago, the empirical value was still compatible with the exact number 137. Many physicists, including Dirac and Heisenberg, have puzzled over whether there is a special reason behind this number. Arthur S. Eddington, who is widely known for measuring the deflection of light near the sun in 1919, published an obscure derivation in 1918, according to which the exact value should be 136. He later came to a modified theory with the exact value 137, in which he also gave a formula for the exact number of protons in the universe. However, these numerological experiments should not be taken seriously.
Wolfgang Pauli also suspected a deeper reason for the value 137. He even discussed with the psychoanalyst C.G. Jung the possible special meaning of the number 137, and related it with the Kabbalah. Before his death in 1958, he was placed in room number 137 in a hospital in Zurich, which really worried him.
There are numerous attempts to represent the value of the fine structure constant using simple formulas. For example, A. Wyler published the following expression for this in 1969:
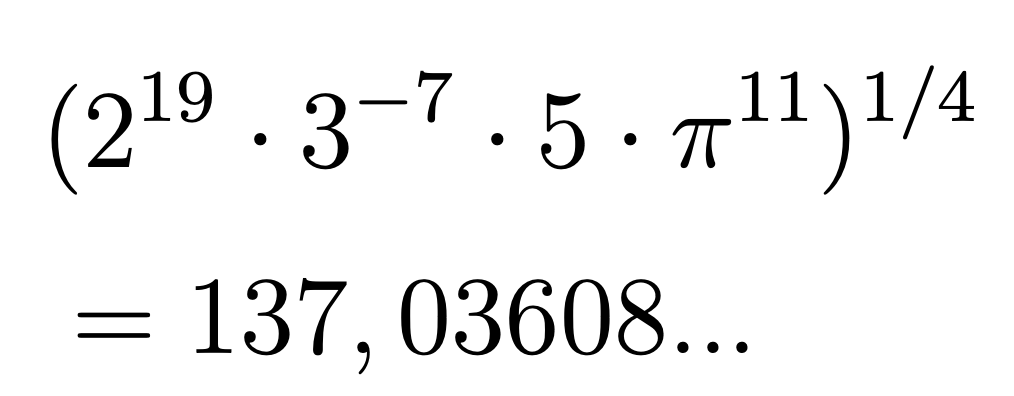
However, it turns out that you can find many such formulas without there being anything behind them.
Today we know that the "fine structure constant" depends on the energy of the processes under consideration and increases at high energies. This means that the meaning of the numerical value 137 has been put into perspective.
Finally, a story. When Pauli went to heaven, he demanded to speak to God, and asked him about the value of the fine structure constant. God pulled out a stack of notes and began calculating on the board. After three minutes, Pauli shouted "That's wrong!"
A. If you insert the numbers n=1, 2, 3, etc. up to n=40 into the quadratic expression n2 - n + 41, you get prime numbers. Leonhard Euler observed this in 1772.
B. The number exp( π √163 ) = 262537412640768743.99999999999925... is almost exactly an integer.
Fun fact: the two issues are related.
1. The solutions to the quadratic equation x2 - x + 41 = 0 with Euler's polynomial are the complex numbers 1/2 ± i/2 √163, with the prime number 163. Adding integer coefficients k and m, one obtains the number system, which consists of the complex numbers of the form k/2 + i m/2 √163. These can be added, subtracted, multiplied and divided within the system.
2. In number systems of a similar type with a number d instead of 163, the uniqueness of the prime factorization does not always apply. In 1801, in his monumental youth work "Disquisitiones arithmeticae", Gauss proved results which are equivalent to the fact that the prime factorization in the number system mentioned above is unique for the 9 prime numbers: 1, 2, 3, 7, 11, 19, 43, 67 and 163. These are called Heegner numbers (see below), although they should actually be named after Gauss. It can be shown that this result implies fact A.
3. In complex analysis there is a prominent function, Felix Klein's "modular invariant" j(t). In his "Textbook of Algebra" Heinrich Weber showed in 1895 that j(t) is an integer if t = 1/2 + i/2 sqrt(d) and d is one of the Heegner numbers above. j(t) has a series expansion with the leading term exp(-2 π i t). This then implies that exp( π √163 ) is almost exactly an integer.
4. Are there other Heegner numbers beyond 163? A number of prominent mathematicians had already addressed this problem when, in 1952, retired engineer and mathematician Kurt Heegner published a sophisticated proof that 163 was the largest. However, there were gaps in the proof. Other, more complete proofs were provided by Harold Stark and Alan Baker in 1966. The gaps in Heegner's proof were filled by Stark in 1969.
If we do the same investigation with the number 18, we find that 5, 7, 11, 13 and 17 are coprime to 18. This time they are all prime numbers.
Question: for which numbers N it is true that all numbers smaller than N that are coprime to N are prime numbers?
By trying you find 3, 4, 6, 8, 12, 18, 24 and 30. They are also called "very round numbers". Are there any others?
In fact, 30 is the largest "very round" number. A proof of this was found in 1907 by the Münster student Bonse. It is relatively easy to see that for n>3 it is sufficient to show the inequality (pn+1)2 < p1 p2 ... pn, where pn is the sequence of prime numbers. However, proving this inequality using elementary means, i.e. without the heavy artillery of analytical number theory, is difficult.
Literature:
H. Rademacher and O. Toeplitz, The Enjoyment of Math, Princeton University Press, 1966, Chapter 22.
R. Honsberger, Mathematical Gems, The Two-Year College Mathematics Journal 10 (1979) 195-197.
The On-Line Encyclopedia of Integer Sequences, Sequence A048597.
In how many ways Mn can you seat n married couples at a round table if each woman is supposed to sit between two men, but no woman is supposed to sit next to her own husband?
This problem comes from the mathematician E. Lucas (1842-1891). By trial you find M2 = 0, M3 = 12 and M4 = 96. Is there a general formula for Mn?
The problem has been solved by mathematicians. It turns out that the solution is quite complicated. The number of ways the women can place themselves is easy to find. It is 2 n! ("2 times n factorial"). But the number An of possibilities for then placing the men defies an elementary solution.
After lengthy considerations, Laisant found a recursion formula in 1891:
(n - 1) An+1 = (n2 -1) An + (n + 1) An-1 + 4 (-1)n.
After all, it can be used to calculate the values of An, e.g. A3 = 1, A4 = 2, A5 = 13, A6 = 80, etc., and from this Mn = 2 n! An, namely M3 = 12, M4 = 96, M5 = 3120, M6 = 115200, etc.
Is there a closed formula for this? Yes, it is
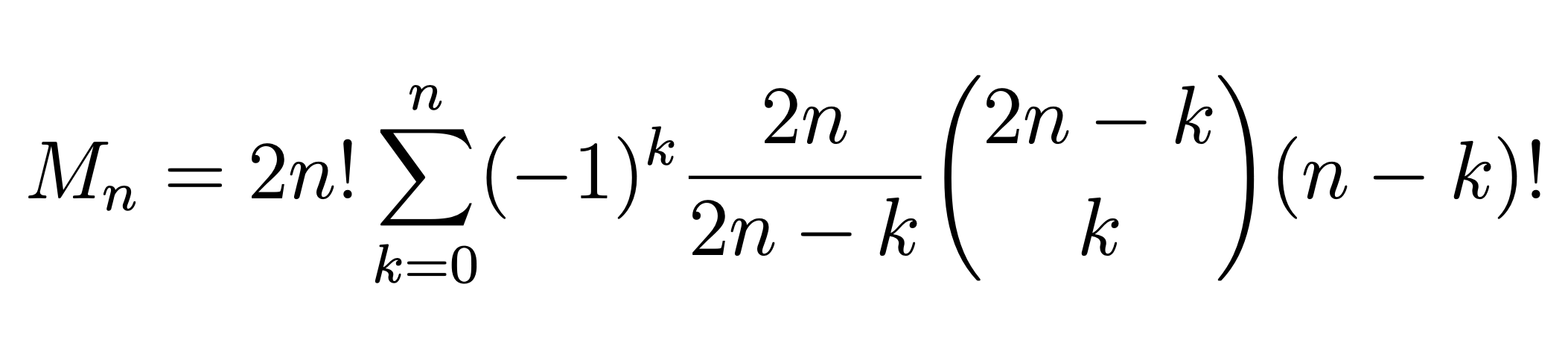
but unfortunately it is a complicated sum that does not make the calculation any easier.