


Next: Acknowledgements
Up: Bayesian Field Theory Nonparametric
Previous: A numerical example
Many nonparametric real world learning problems
are generically non-Gaussian.
Examples include general density estimation
or the reconstruction of forces for quantum systems
from observational data.
Increasing computational resources
allow to solve at least some
of such low-dimensional non-Gaussian
problems directly by discretization.
Figure 1:
(a):
True conditional likelihood
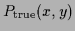 =
=
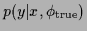 .
(b):
Corresponding true field,
here chosen as (conditional) log-likelihood
.
(b):
Corresponding true field,
here chosen as (conditional) log-likelihood  =
=  , i.e.,
, i.e.,
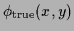 =
=
 =
=
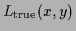 .
.
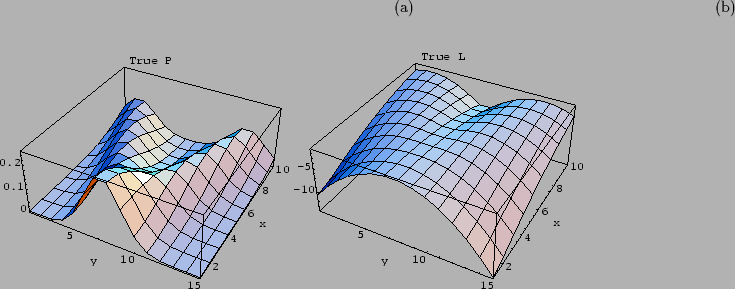 |
Figure 2:
(a):
Conditional empirical density
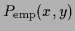 =
=
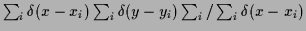 ,
as obtained from 50 data points
sampled from the true likelihood
,
as obtained from 50 data points
sampled from the true likelihood 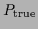 of Fig. 1a under uniform
of Fig. 1a under uniform 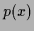 .
(b): Conditional likelihood
.
(b): Conditional likelihood 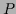 reconstructed from the conditional empirical density
shown on the l.h.s. using, besides the normalization constraint,
an additional Gaussian prior term on
reconstructed from the conditional empirical density
shown on the l.h.s. using, besides the normalization constraint,
an additional Gaussian prior term on  (see text).
(see text).
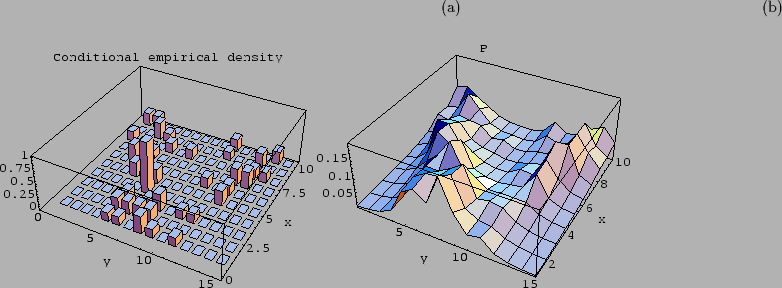 |
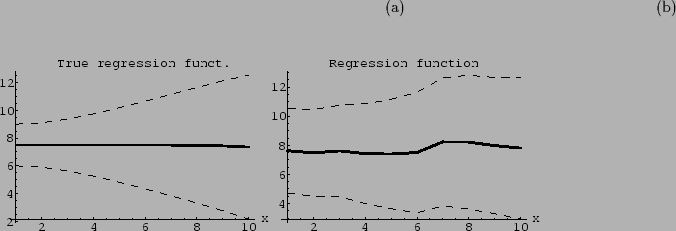
Figure 3:
(a): Regression function for 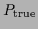 of Fig. 1a.
(b): Regression function for the reconstructed
of Fig. 1a.
(b): Regression function for the reconstructed 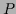 of Fig. 2b.
(The regression function for a field
of Fig. 2b.
(The regression function for a field  is defined as
is defined as
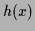 =
=
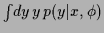 .
The dashed lines indicate the range of
one standard deviation above and below the regression function.)
.
The dashed lines indicate the range of
one standard deviation above and below the regression function.)
 |
Subsections



Next: Acknowledgements
Up: Bayesian Field Theory Nonparametric
Previous: A numerical example
Joerg_Lemm
2000-09-12



