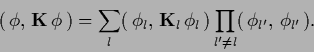Next: Decision trees
Up: Parameterizing likelihoods: Variational methods
Previous: Additive models
Contents
A product ansatz has the form
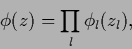 |
(403) |
where
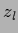 =
=
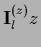 represents projections
of the vector
represents projections
of the vector 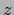 consisting of all
consisting of all  and
and  components.
The ansatz can be made more flexible by using sum of products
components.
The ansatz can be made more flexible by using sum of products
 |
(404) |
The restriction of the trial space to product functions
corresponds to the Hartree approximation in physics.
(In a Hartree-Fock approximation
the product functions are antisymmetrized under coordinate exchange.)
For additive 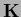 =
=
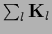 with
with 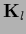 acting only on
acting only on 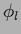 , i.e.,
, i.e.,
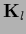 =
=
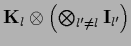 ,
with
,
with 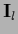 the projector into the space of functions
the projector into the space of functions
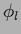 =
=
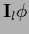 ,
the quadratic regularization term becomes,
assuming
,
the quadratic regularization term becomes,
assuming 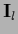
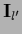 =
=
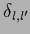 ,
,
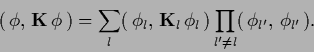 |
(405) |
For 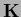 =
=
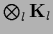 with a product structure with respect to
with a product structure with respect to 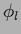
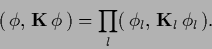 |
(406) |
In both cases the prior term factorizes into lower dimensional
contributions.




Next: Decision trees
Up: Parameterizing likelihoods: Variational methods
Previous: Additive models
Contents
Joerg_Lemm
2001-01-21
![]() =
=
![]() with
with ![]() acting only on
acting only on ![]() , i.e.,
, i.e.,
![]() =
=
![]() ,
with
,
with ![]() the projector into the space of functions
the projector into the space of functions
![]() =
=
![]() ,
the quadratic regularization term becomes,
assuming
,
the quadratic regularization term becomes,
assuming ![]()
![]() =
=
![]() ,
,