A Laplacian smoothness prior, for example,
can be related to
an approximate symmetry
under infinitesimal translations.
Considering the group of
![]() -dimensional translations which is generated
by the gradient operator
-dimensional translations which is generated
by the gradient operator ![]() ,
this can be verified by recalling the multidimensional Taylor formula
for expansion of
,
this can be verified by recalling the multidimensional Taylor formula
for expansion of ![]() at
at ![]()
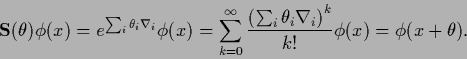 |
(218) |
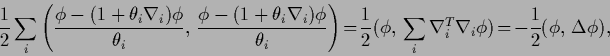 |
(219) |