



Next: Approximate symmetries
Up: Covariances and invariances
Previous: Covariances and invariances
Contents
Prior terms can often be related to
the assumption of
approximate invariances
or approximate symmetries.
A Laplacian smoothness functional, for example,
measures the deviation from translational symmetry
under infinitesimal translations.
Consider for example a linear mapping
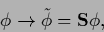 |
(208) |
given by the operator 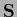 .
To compare
.
To compare  with
with 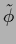 we define a (semi-)distance defined by choosing a
positive (semi-)definite
we define a (semi-)distance defined by choosing a
positive (semi-)definite 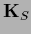 ,
and use as error measure
,
and use as error measure
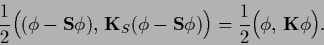 |
(209) |
Here
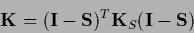 |
(210) |
is positive semi-definite
if 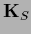 is.
Conversely, every positive semi-definite K
can be written
is.
Conversely, every positive semi-definite K
can be written
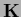 =
=
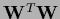 and is thus of form (210) with
and is thus of form (210) with
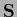 =
=
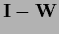 and
and
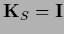 .
Including terms of the form of (210)
in the error functional forces
.
Including terms of the form of (210)
in the error functional forces  to be similar to
to be similar to 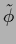 .
.
A special case are mappings
leaving the norm invariant
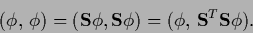 |
(211) |
For real  and
and 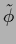 i.e.,
i.e., 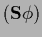 =
=
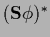 ,
this requires
,
this requires
 and
and
 .
Thus, in that case
.
Thus, in that case
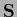 has to be an orthogonal matrix
has to be an orthogonal matrix
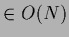 and can be written
and can be written
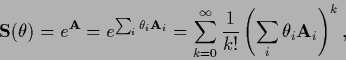 |
(212) |
with antisymmetric
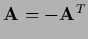 and real parameters
and real parameters  .
Selecting a set of
(generators)
.
Selecting a set of
(generators) 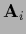 the matrices obtained be varying the parameters
the matrices obtained be varying the parameters  form a Lie group.
Up to first order the expansion of the exponential function reads
form a Lie group.
Up to first order the expansion of the exponential function reads
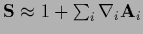 .
Thus, we can define an error measure with respect to an
infinitesimal transformation by
.
Thus, we can define an error measure with respect to an
infinitesimal transformation by
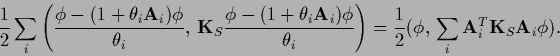 |
(213) |




Next: Approximate symmetries
Up: Covariances and invariances
Previous: Covariances and invariances
Contents
Joerg_Lemm
2001-01-21