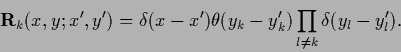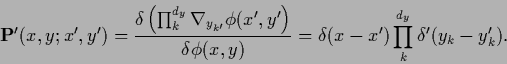Next: Covariances and invariances
Up: General Gaussian prior factors
Previous: Example: Square root of
Contents
Instead in terms of the probability density function,
one can formulate the prior in terms of its integral,
the distribution function. The density 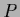 is then recovered
from the distribution function
is then recovered
from the distribution function 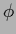 by differentiation,
by differentiation,
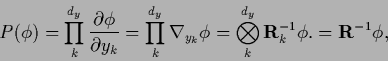 |
(203) |
resulting in a non-diagonal
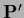 .
The inverse of the derivative operator
.
The inverse of the derivative operator 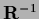 is
the integration operator
is
the integration operator 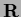 =
=
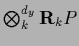 with matrix elements
with matrix elements
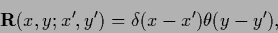 |
(204) |
i.e.,
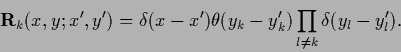 |
(205) |
Thus, (203)
corresponds to the transformation of (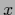 -conditioned)
density functions
-conditioned)
density functions 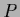 in (
in (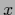 -conditioned)
distribution functions
-conditioned)
distribution functions
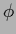 =
= 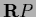 , i.e.,
, i.e.,
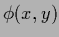 =
=
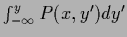 .
Because
.
Because
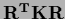 is positive (semi-)definite
if
is positive (semi-)definite
if 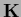 is,
a specific prior which is Gaussian in the distribution function
is,
a specific prior which is Gaussian in the distribution function 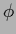 is also Gaussian in the density
is also Gaussian in the density 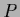 .
.
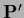 becomes
becomes
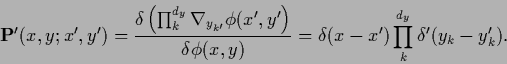 |
(206) |
Here the derivative of the 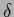 -function is defined
by formal partial integration
-function is defined
by formal partial integration
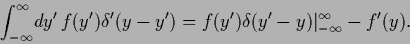 |
(207) |
Fixing
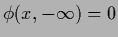 the variational derivative
the variational derivative
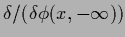 is not needed.
The normalization condition for
is not needed.
The normalization condition for 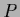 becomes
for the distribution function
becomes
for the distribution function 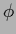 =
= 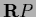 the boundary condition
the boundary condition
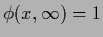 ,
,
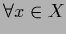 .
The non-negativity condition for
.
The non-negativity condition for 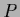 corresponds
to the monotonicity condition
corresponds
to the monotonicity condition
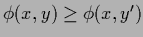 ,
,
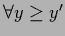 ,
,
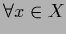 and to
and to
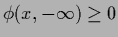 ,
,
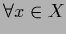 .
.




Next: Covariances and invariances
Up: General Gaussian prior factors
Previous: Example: Square root of
Contents
Joerg_Lemm
2001-01-21
![]() is then recovered
from the distribution function
is then recovered
from the distribution function ![]() by differentiation,
by differentiation,