



Next: An Example: Regression
Up: The Bayesian approach
Previous: The Bayesian approach
Contents
A Bayesian approach is based upon two main ingredients:
- 1.
- A model of Nature, i.e., a space
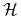 of hypotheses
of hypotheses 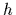 defined by their likelihood functions
defined by their likelihood functions
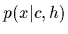 .
Likelihood functions specify
the probability density
for producing outcome
.
Likelihood functions specify
the probability density
for producing outcome 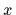 (measured value or dependent visible variable,
assumed to be directly observable)
under hypothesis
(measured value or dependent visible variable,
assumed to be directly observable)
under hypothesis 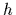 (possible state of Nature or hidden variable, assumed to be not directly observable)
and condition
(possible state of Nature or hidden variable, assumed to be not directly observable)
and condition 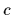 (measurement device parameters or independent visible variable,
assumed to be directly observable).
(measurement device parameters or independent visible variable,
assumed to be directly observable).
- 2.
- A prior density
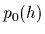 =
= 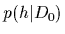 defined over the space
defined over the space 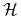 of hypotheses,
of hypotheses,
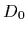 denoting collectively all available a priori information.
denoting collectively all available a priori information.
Now assume (new) training data
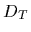 =
= 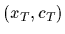 =
=
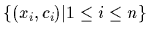 become available,
consisting of pairs
of measured values
become available,
consisting of pairs
of measured values 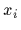 under known conditions
under known conditions 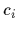 (and unknown
(and unknown 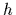 ).
Then
Bayes' theorem
).
Then
Bayes' theorem
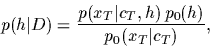 |
(1) |
is used to update
the prior density 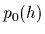 =
= 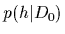 to get the (new)
posterior density
to get the (new)
posterior density 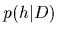 =
= 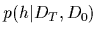 .
Here we wrote
.
Here we wrote 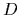 =
= 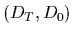 to denote both,
training data and a priori information.
Assuming i.i.d. training data
to denote both,
training data and a priori information.
Assuming i.i.d. training data 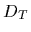 the likelihoods factorize
the likelihoods factorize
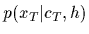 =
=
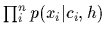 .
Note that the denominator which appears in Eq. (1),
i.e.,
.
Note that the denominator which appears in Eq. (1),
i.e., 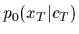 =
=
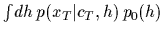 ,
is
,
is 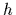 -independent.
It plays the role of a normalization factor,
also known as evidence.
Thus, the terms in Eq. (1)
are named as follows,
-independent.
It plays the role of a normalization factor,
also known as evidence.
Thus, the terms in Eq. (1)
are named as follows,
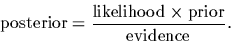 |
(2) |
To make predictions,
a Bayesian approach aims at calculating
the predictive density
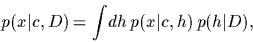 |
(3) |
which is a likelihood average
weighted by their posterior probability.
The 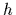 -integral can be extremely high dimensional,
and often, like in the case we are focusing on here,
even be a functional integral [39,40]
over a space of likelihood functions
-integral can be extremely high dimensional,
and often, like in the case we are focusing on here,
even be a functional integral [39,40]
over a space of likelihood functions 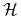 .
In as far as an analytical integration is not possible,
one has to treat the integral, for example,
by Monte Carlo methods
[30, 41-44] or in saddle point approximation
[26,30,45,46].
Assuming the likelihood term
.
In as far as an analytical integration is not possible,
one has to treat the integral, for example,
by Monte Carlo methods
[30, 41-44] or in saddle point approximation
[26,30,45,46].
Assuming the likelihood term 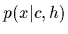 to be
slowly varying at the stationary point
the latter is also known
as maximum posterior approximation.
In this approximation the
to be
slowly varying at the stationary point
the latter is also known
as maximum posterior approximation.
In this approximation the 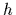 -integration is effectively replaced
by a maximization of the posterior,
meaning the predictive density is approximated by
-integration is effectively replaced
by a maximization of the posterior,
meaning the predictive density is approximated by
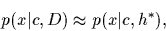 |
(4) |
where
![\begin{displaymath}
h^*
= {\rm argmax}_{h\in{\cal H}} p(h\vert D)
= {\rm argmin}_{h\in{\cal H}} [-\ln p(h\vert D)]
.
\end{displaymath}](img96.gif) |
(5) |
The term 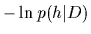 is also often referred to as
(regularized) error functional
and indeed, a maximum posterior approximation
is technically equivalent to minimizing
error functionals with Tikhonov regularization
[2-4, 47]. The difference between the Bayesian approach
and the classical Tikhonov regularization
is the interpretation of the extra term
as costs or as a priori information, respectively.
is also often referred to as
(regularized) error functional
and indeed, a maximum posterior approximation
is technically equivalent to minimizing
error functionals with Tikhonov regularization
[2-4, 47]. The difference between the Bayesian approach
and the classical Tikhonov regularization
is the interpretation of the extra term
as costs or as a priori information, respectively.
Within a
maximum likelihood approach
an optimal hypothesis 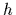 is obtained by
maximizing only its training likelihood
is obtained by
maximizing only its training likelihood 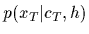 instead of its complete posterior.
This is equivalent to a maximum posterior approximation
with uniform prior density.
A maximum likelihood approach
can be used for hypotheses
instead of its complete posterior.
This is equivalent to a maximum posterior approximation
with uniform prior density.
A maximum likelihood approach
can be used for hypotheses 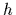 =
= 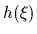 ,
parameterized by (vectors)
,
parameterized by (vectors) 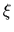 .
A maximum likelihood approach is possible
if that parameterization is restrictive enough
(and well enough adapted to the problem),
so no additional prior is required to
allow generalization from training
to non-training data.
For completely flexible nonparametric approaches, however,
the prior term is necessary
to provide the necessary information
linking training data and (future) non-training data.
Indeed,
if every number
.
A maximum likelihood approach is possible
if that parameterization is restrictive enough
(and well enough adapted to the problem),
so no additional prior is required to
allow generalization from training
to non-training data.
For completely flexible nonparametric approaches, however,
the prior term is necessary
to provide the necessary information
linking training data and (future) non-training data.
Indeed,
if every number 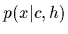 is considered
as a single degree of freedom
[restricted only by the positivity constraint
is considered
as a single degree of freedom
[restricted only by the positivity constraint 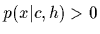 and the normalization over
and the normalization over 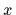 ]
then, without a priori information,
training data contain no information
about non-training data.
]
then, without a priori information,
training data contain no information
about non-training data.




Next: An Example: Regression
Up: The Bayesian approach
Previous: The Bayesian approach
Contents
Joerg_Lemm
2000-06-06
![]() =
= ![]() =
=
![]() become available,
consisting of pairs
of measured values
become available,
consisting of pairs
of measured values ![]() under known conditions
under known conditions ![]() (and unknown
(and unknown ![]() ).
Then
Bayes' theorem
).
Then
Bayes' theorem
![]() is obtained by
maximizing only its training likelihood
is obtained by
maximizing only its training likelihood ![]() instead of its complete posterior.
This is equivalent to a maximum posterior approximation
with uniform prior density.
A maximum likelihood approach
can be used for hypotheses
instead of its complete posterior.
This is equivalent to a maximum posterior approximation
with uniform prior density.
A maximum likelihood approach
can be used for hypotheses ![]() =
= ![]() ,
parameterized by (vectors)
,
parameterized by (vectors) ![]() .
A maximum likelihood approach is possible
if that parameterization is restrictive enough
(and well enough adapted to the problem),
so no additional prior is required to
allow generalization from training
to non-training data.
For completely flexible nonparametric approaches, however,
the prior term is necessary
to provide the necessary information
linking training data and (future) non-training data.
Indeed,
if every number
.
A maximum likelihood approach is possible
if that parameterization is restrictive enough
(and well enough adapted to the problem),
so no additional prior is required to
allow generalization from training
to non-training data.
For completely flexible nonparametric approaches, however,
the prior term is necessary
to provide the necessary information
linking training data and (future) non-training data.
Indeed,
if every number ![]() is considered
as a single degree of freedom
[restricted only by the positivity constraint
is considered
as a single degree of freedom
[restricted only by the positivity constraint ![]() and the normalization over
and the normalization over ![]() ]
then, without a priori information,
training data contain no information
about non-training data.
]
then, without a priori information,
training data contain no information
about non-training data.