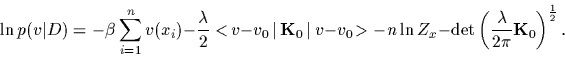Next: Inverse many-body theory
Up: Inverse quantum statistics
Previous: Inverse two-body problems
Contents
Before discussing a possible approximation for many-body systems
we will first study the classical
limit of inverse quantum statistics.
The classical limit is much easier to solve than the full
quantum mechanical problem
and may, for example for large masses,
already give a useful approximation.
The phase space density of a classical canonical ensemble
is given by
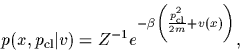 |
(55) |
with
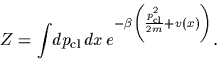 |
(56) |
Here we used 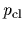 to denote the classical momentum
to distinguish it from a density
to denote the classical momentum
to distinguish it from a density 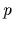 .
The probability
.
The probability
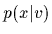 for measuring
for measuring 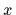 [to simplify the notation
we abstain in this context from denoting the observable
[to simplify the notation
we abstain in this context from denoting the observable 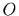 explicitly]
is then obtained by integrating over
explicitly]
is then obtained by integrating over 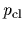 ,
,
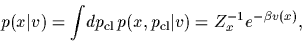 |
(57) |
where
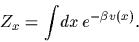 |
(58) |
Notice, that the classical 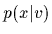 is mass independent,
and, most important,
that it can be obtained directly from
is mass independent,
and, most important,
that it can be obtained directly from 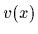 without having to solve an eigenvalue problem
like in the quantum case.
without having to solve an eigenvalue problem
like in the quantum case.
Analogously to the quantum mechanical approach
the classical likelihood model (57)
for position measurements
can now be combined with a prior model for potentials 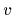 ,
leading to a posterior density
,
leading to a posterior density 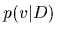 .
In particular, adding a Gaussian process prior
the log-posterior becomes
.
In particular, adding a Gaussian process prior
the log-posterior becomes
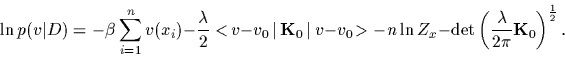 |
(59) |
Again, we may refer to a maximum posterior approximation
and consider the potential which maximizes the posterior
as the solution of our reconstruction problem.
The corresponding stationarity equation
is found by setting
the functional derivative of the log-posterior
with respect to 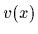 to zero,
to zero,
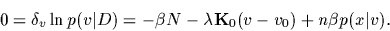 |
(60) |
Choosing an initial guess 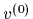 Eq. (60) can be solved
by straightforward iteration.
The results of a classical calculation
(with parameters and data as
in Fig. 4, but without energy penalty term)
are shown in Fig. 8.
Eq. (60) can be solved
by straightforward iteration.
The results of a classical calculation
(with parameters and data as
in Fig. 4, but without energy penalty term)
are shown in Fig. 8.
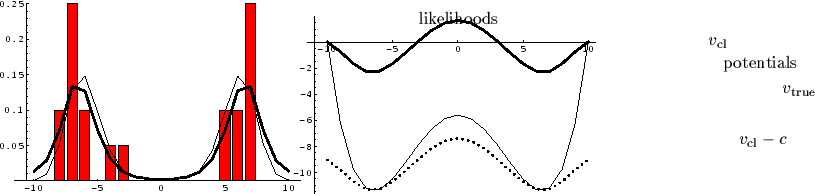
Figure 8:
Classical approximation of symmetric potential.
Shown are likelihoods (left hand side)
and potentials (right hand side):
Original likelihood and potential (thin lines),
approximated likelihood and potential 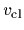 (thick lines),
empirical density (bars).
The dotted line shows
(thick lines),
empirical density (bars).
The dotted line shows
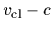 with constant
with constant
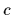 =
=
![${\rm min}[v_{\rm cl}]-{\rm min}[v_{\rm true}]$](img356.gif) .
Except for the fact that no
energy penalty term has been used for this classical calculation
the parameters and data are
the same as in Fig. 4.
(20 data points, sampled from the true quantum mechanical likelihood,
truncated RBF covariances (54) with
.
Except for the fact that no
energy penalty term has been used for this classical calculation
the parameters and data are
the same as in Fig. 4.
(20 data points, sampled from the true quantum mechanical likelihood,
truncated RBF covariances (54) with
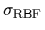 =
= 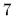 ,
,
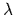 =
= 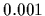 ,
inverse physical temperature
,
inverse physical temperature 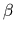 = 1,
= 1,
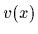 =
= 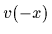 and
and
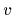 = 0 at the boundaries.)
= 0 at the boundaries.)
 |




Next: Inverse many-body theory
Up: Inverse quantum statistics
Previous: Inverse two-body problems
Contents
Joerg_Lemm
2000-06-06
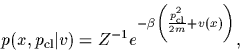
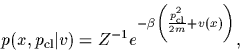
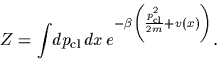
![]() ,
leading to a posterior density
,
leading to a posterior density ![]() .
In particular, adding a Gaussian process prior
the log-posterior becomes
.
In particular, adding a Gaussian process prior
the log-posterior becomes