Stochastic process priors have, compared to priors over parameters ![]() ,
the advantage of implementing a priori knowledge explicitly
in terms of the function values
,
the advantage of implementing a priori knowledge explicitly
in terms of the function values ![]() .
Gaussian processes, in particular, always correspond
to simple quadratic error surfaces, i.e., concave densities.
Being technically very convenient, this is,
on the other hand, a strong restriction.
Arbitrary prior processes, however, can easily
be built by using mixtures of Gaussian processes
without loosing the advantage of an explicit prior implementation
[32,33,63,67].
(We want
to point out that using a mixture of Gaussian process priors
does not restrict
.
Gaussian processes, in particular, always correspond
to simple quadratic error surfaces, i.e., concave densities.
Being technically very convenient, this is,
on the other hand, a strong restriction.
Arbitrary prior processes, however, can easily
be built by using mixtures of Gaussian processes
without loosing the advantage of an explicit prior implementation
[32,33,63,67].
(We want
to point out that using a mixture of Gaussian process priors
does not restrict ![]() to a mixture of Gaussians.)
to a mixture of Gaussians.)
A mixture of ![]() Gaussian processes
with component means
Gaussian processes
with component means ![]() and
inverse component covariances
and
inverse component covariances
![]() reads
reads
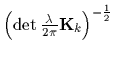 and mixture probabilities
and mixture probabilities