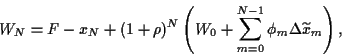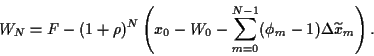Nächste Seite: Literatur
Aufwärts: Der ``faire'' Preis eines
Vorherige Seite: No-Arbitrage-Prinzip
Inhalt
Um die Behandlung von Optionen vorzubereiten
und die grundlegenden Begriffe einzuführen
leiten wir den fairen Preis eines Forwardkontraktes
nocheinmal etwas formaler her.
(Die Vorgehensweise entspricht der in [2].)
Es seien 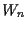 das Gesamtvermögen eines Akteurs zum Zeitpunkt
das Gesamtvermögen eines Akteurs zum Zeitpunkt 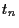 ,
von dem wir nun annehmen, daß es sich aufteilt
in Barvermögen
,
von dem wir nun annehmen, daß es sich aufteilt
in Barvermögen 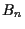 und
und
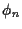 Anteile eines frei handelbaren Underlyings
(von welchem wir nun annehmen es handele sich um eine Aktie)
mit einem Stückpreis (Kurs zum Zeitpunkt
Anteile eines frei handelbaren Underlyings
(von welchem wir nun annehmen es handele sich um eine Aktie)
mit einem Stückpreis (Kurs zum Zeitpunkt 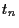 ) von
) von 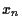 .
Für das Gesamtvermögen zum Zeitpunkt
.
Für das Gesamtvermögen zum Zeitpunkt 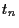 gilt also
gilt also
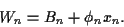 |
(4) |
Weiterhin nehmen wir an,
dem betrachteten Akteur
stehe eine risikolose Anlageform für sein Geldvermögen zur Verfügung
mit dem Zinssatz 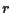 .
Konkret heißt das, in dem Zeitraum
.
Konkret heißt das, in dem Zeitraum
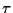 =
= 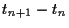 ,
vermehre sich das Geldvermögen
,
vermehre sich das Geldvermögen 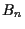 um den Betrag
um den Betrag
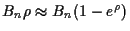 ,
wobei
,
wobei 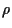 =
= 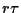 .
Der Wert des Aktienvermögens ändert sich dagegen
durch Änderung der Kurse
.
Der Wert des Aktienvermögens ändert sich dagegen
durch Änderung der Kurse 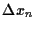 =
= 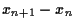 .
.
Zur formalen Beschreibung ist es hilfreich
die zeitliche Entwicklung
des Vermögens 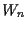 in zwei Schritte zu unterteilen:
(a) die zeitliche Veränderung des Vermögens
durch Verzinsung des Geldes einerseits und
die Veränderung des Aktienkurses andererseits.
(b) die (instantane) Umschichtung des Vermögens
zwischen Bargeld und Aktien.
Dies führt auf folgendes Modell:
in zwei Schritte zu unterteilen:
(a) die zeitliche Veränderung des Vermögens
durch Verzinsung des Geldes einerseits und
die Veränderung des Aktienkurses andererseits.
(b) die (instantane) Umschichtung des Vermögens
zwischen Bargeld und Aktien.
Dies führt auf folgendes Modell:
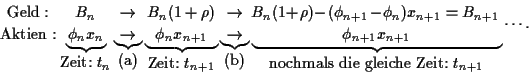 |
(5) |
(a) Die zeitliche Entwicklung des Vermögens
in der Zeit 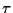 =
= 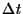 =
= 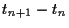 ist daher
ist daher
wobei 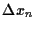 =
= 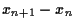 .
und
.
und 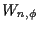 =
= 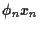 .
.
(b) Eine Vermögensumschichtung
bedeutet Aktienkauf bei Verminderung des Barvermögens
bzw. Aktienverkauf bei Erhöhung des Barvermögens,
wobei
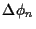 =
=
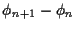 .
Die Vermgensumschichtung selbst
ist erfolgsneutral
.
Die Vermgensumschichtung selbst
ist erfolgsneutral
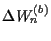 = 0.
Insgesamt erhalten wir daher für die Änderung
des Vermögens
= 0.
Insgesamt erhalten wir daher für die Änderung
des Vermögens
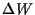 =
=
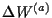 , d.h.,
, d.h.,
Durch Iteration folgt
mit diskontierten (auf 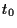 abgezinsten)
abgezinsten)
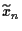 =
=
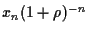 .
Damit erhalten wir ebenfalls
.
Damit erhalten wir ebenfalls
Hierbei haben wir benutzt, daß 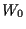 =
= 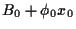 ,
und,
als diskretes Analogon einer partiellen Integration,
,
und,
als diskretes Analogon einer partiellen Integration,
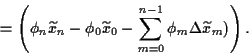 |
(15) |
Addieren wir für den Schlußabrechnungstag (zur Zeit 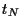 )
noch die Vermögensänderung durch den zu erfüllenden Terminkontrakt
(
)
noch die Vermögensänderung durch den zu erfüllenden Terminkontrakt
(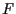 -
- 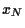 aus der Sicht einer Short-Position),
so erhalten wir
aus der Sicht einer Short-Position),
so erhalten wir
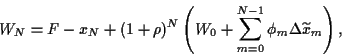 |
(16) |
oder, mit
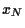 =
=
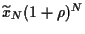 und
und
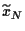 =
=
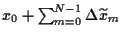 ,
,
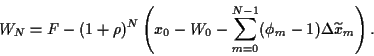 |
(17) |
Wir erkennen, daß die Wahl
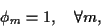 |
(18) |
den Tradingterm vollständig eliminiert.
Damit werden auch alle Zufallfaktoren,
d.h. die probabilistische Entwicklung
der Aktienkurse 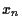 eliminiert.
Die Wahl
eliminiert.
Die Wahl 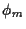 =
= 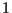 minimiert also das Risiko
für den Halter der Short-Position.
Dies entspricht einer Hedgestrategie
bei dem das Underlying zu Beginn, d.h. zur Zeit
minimiert also das Risiko
für den Halter der Short-Position.
Dies entspricht einer Hedgestrategie
bei dem das Underlying zu Beginn, d.h. zur Zeit 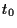 ,
gekauft und bis zum Ende
,
gekauft und bis zum Ende 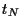 gehalten wird.
Unter diesen Umständen ergibt sich
gehalten wird.
Unter diesen Umständen ergibt sich
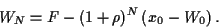 |
(19) |
Ein ``fairer'' Preis 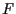 entspricht der Bedingung,
entspricht der Bedingung,
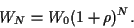 |
(20) |
Es folgt
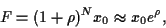 |
(21) |
d.h. der faire Forwardpreis
entspricht dem aufgezinsten
Preis des Underlying zum Zeitpunkt 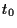 .
Falls der Forwardpreis dieser Bedingung nicht genügt,
sind daher Arbitragegewinne möglich.
Idealerweise sorgen also entsprechende Arbitrageure dafür, daß sich
dieser Preis am Markt einstellt.
In der Praxis können allerdings z.B. nichtverschwindende Transaktionskosten und ein variables Zinsniveau
.
Falls der Forwardpreis dieser Bedingung nicht genügt,
sind daher Arbitragegewinne möglich.
Idealerweise sorgen also entsprechende Arbitrageure dafür, daß sich
dieser Preis am Markt einstellt.
In der Praxis können allerdings z.B. nichtverschwindende Transaktionskosten und ein variables Zinsniveau 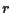 zu Abweichungen führen.
zu Abweichungen führen.




Nächste Seite: Literatur
Aufwärts: Der ``faire'' Preis eines
Vorherige Seite: No-Arbitrage-Prinzip
Inhalt
Joerg_Lemm
2000-02-01
![]() das Gesamtvermögen eines Akteurs zum Zeitpunkt
das Gesamtvermögen eines Akteurs zum Zeitpunkt ![]() ,
von dem wir nun annehmen, daß es sich aufteilt
in Barvermögen
,
von dem wir nun annehmen, daß es sich aufteilt
in Barvermögen ![]() und
und
![]() Anteile eines frei handelbaren Underlyings
(von welchem wir nun annehmen es handele sich um eine Aktie)
mit einem Stückpreis (Kurs zum Zeitpunkt
Anteile eines frei handelbaren Underlyings
(von welchem wir nun annehmen es handele sich um eine Aktie)
mit einem Stückpreis (Kurs zum Zeitpunkt ![]() ) von
) von ![]() .
Für das Gesamtvermögen zum Zeitpunkt
.
Für das Gesamtvermögen zum Zeitpunkt ![]() gilt also
gilt also
![]() in zwei Schritte zu unterteilen:
(a) die zeitliche Veränderung des Vermögens
durch Verzinsung des Geldes einerseits und
die Veränderung des Aktienkurses andererseits.
(b) die (instantane) Umschichtung des Vermögens
zwischen Bargeld und Aktien.
Dies führt auf folgendes Modell:
in zwei Schritte zu unterteilen:
(a) die zeitliche Veränderung des Vermögens
durch Verzinsung des Geldes einerseits und
die Veränderung des Aktienkurses andererseits.
(b) die (instantane) Umschichtung des Vermögens
zwischen Bargeld und Aktien.
Dies führt auf folgendes Modell:
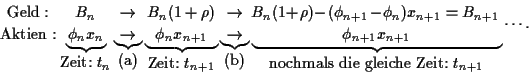
![]() =
= ![]() =
= ![]() ist daher
ist daher
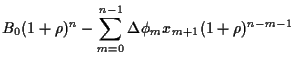
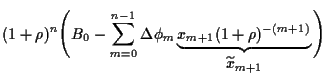
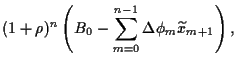

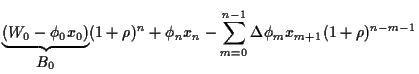
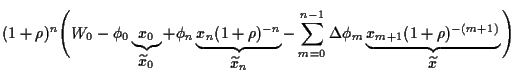
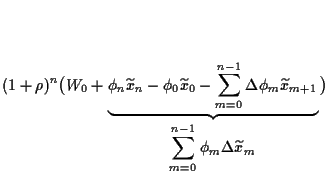
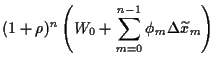
![$\displaystyle (1+\rho)^n\left(
W_0+\sum_{m=0}^{n-1}\phi_m [\widetilde x_{m+1}-\widetilde x_m]
\right)$](img89.gif)
^{n-m-1}
.$](img90.gif)
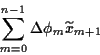
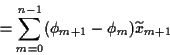
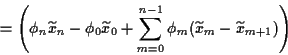
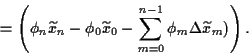
![]() )
noch die Vermögensänderung durch den zu erfüllenden Terminkontrakt
(
)
noch die Vermögensänderung durch den zu erfüllenden Terminkontrakt
(![]() -
- ![]() aus der Sicht einer Short-Position),
so erhalten wir
aus der Sicht einer Short-Position),
so erhalten wir