Next: About this document ... Up: Numerical solution Previous: A numerical scheme
| Space interval | |
| Space discretization step |
|
| Time discretization step |
|
| Amount of time steps | |
| Velocity of the kink |
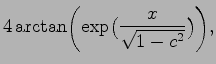 |
|||
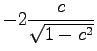 sech sech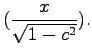 |
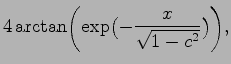 |
|||
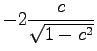 sech sech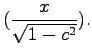 |
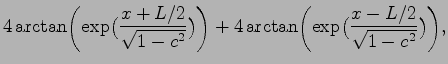 |
|||
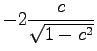 sech sech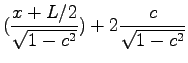 sech sech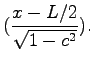 |
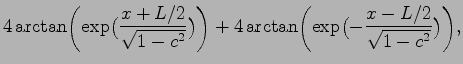 |
|||
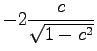 sech sech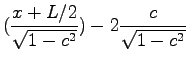 sech sech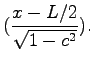 |
Gurevich_Svetlana 2008-11-12