pymor.reductors package

Submodules

basic module

class pymor.reductors.basic.GenericRBReductor(d, RB=None, orthogonal_projection=('initial_data', ), product=None)[source]

Bases: pymor.core.interfaces.BasicInterface

Generic reduced basis reductor.

Replaces each Operator of the given Discretization with the Galerkin projection onto the span of the given reduced basis.

Parameters

d
The Discretization which is to be reduced.
RB
VectorArray containing the reduced basis on which to project.
orthogonal_projection
List of keys in d.operators for which the corresponding Operator should be orthogonally projected (i.e. operators which map to vectors in contrast to bilinear forms which map to functionals).
product
Inner product for the projection of the Operators given by orthogonal_projection.

Methods

GenericRBReductor extend_basis, reconstruct, reduce
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid
extend_basis(U, method='gram_schmidt', pod_modes=1, pod_orthonormalize=True, copy_U=True)[source]

Extend basis by new vectors.

Parameters

U
VectorArray containing the new basis vectors.
method

Basis extension method to use. The following methods are available:

trivial:Vectors in U are appended to the basis. Duplicate vectors in the sense of almost_equal are removed.
gram_schmidt:New basis vectors are orthonormalized w.r.t. to the old basis using the gram_schmidt algorithm.
pod:Append the first POD modes of the defects of the projections of the vectors in U onto the existing basis (e.g. for use in POD-Greedy algorithm).

Warning

In case of the 'gram_schmidt' and 'pod' extension methods, the existing reduced basis is assumed to be orthonormal w.r.t. the given inner product.

pod_modes
In case method == 'pod', the number of POD modes that shall be appended to the basis.
pod_orthonormalize
If True and method == 'pod', re-orthonormalize the new basis vectors obtained by the POD in order to improve numerical accuracy.
copy_U
If copy_U is False, the new basis vectors might be removed from U.

Raises

ExtensionError
Raised when the selected extension method does not yield a basis of increased dimension.
reconstruct(u)[source]

Reconstruct high-dimensional vector from reduced vector u.

reduce()[source]

Perform the reduced basis projection.

Returns

The reduced Discretization.

pymor.reductors.basic.reduce_to_subbasis(d, dim)[source]

Further reduce a Discretization to the subbasis formed by the first dim basis vectors.

This is achieved by calling project_to_subbasis for each operator of the given Discretization.

Parameters

d
The Discretization to further reduce.
dim
The dimension of the subbasis.

Returns

The further reduced Discretization.

coercive module

class pymor.reductors.coercive.CoerciveRBEstimator(residual, residual_range_dims, coercivity_estimator)[source]

Bases: pymor.core.interfaces.ImmutableInterface

Instantiated by CoerciveRBReductor.

Not to be used directly.

Methods

CoerciveRBEstimator estimate, restricted_to_subbasis
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
class pymor.reductors.coercive.CoerciveRBReductor(d, RB=None, orthogonal_projection=('initial_data', ), product=None, coercivity_estimator=None)[source]

Bases: pymor.reductors.basic.GenericRBReductor

Reduced Basis reductor for StationaryDiscretizations with coercive linear operator.

The only addition to GenericRBReductor is an error estimator which evaluates the dual norm of the residual with respect to a given inner product. For the reduction of the residual we use ResidualReductor for improved numerical stability [BEOR14].

[BEOR14](1, 2) A. Buhr, C. Engwer, M. Ohlberger, S. Rave, A Numerically Stable A Posteriori Error Estimator for Reduced Basis Approximations of Elliptic Equations, Proceedings of the 11th World Congress on Computational Mechanics, 2014.

Parameters

d
The Discretization which is to be reduced.
RB
VectorArray containing the reduced basis on which to project.
orthogonal_projection
List of keys in d.operators for which the corresponding Operator should be orthogonally projected (i.e. operators which map to vectors in contrast to bilinear forms which map to functionals).
product
Inner product for the projection of the Operators given by orthogonal_projection and for the computation of Riesz representatives of the residual. If None, the Euclidean product is used.
coercivity_estimator
None or a ParameterFunctional returning a lower bound for the coercivity constant of the given problem. Note that the computed error estimate is only guaranteed to be an upper bound for the error when an appropriate coercivity estimate is specified.

Methods

CoerciveRBReductor reduce
GenericRBReductor extend_basis, reconstruct
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid
class pymor.reductors.coercive.SimpleCoerciveRBEstimator(estimator_matrix, coercivity_estimator)[source]

Bases: pymor.core.interfaces.ImmutableInterface

Instantiated by SimpleCoerciveRBReductor.

Not to be used directly.

Methods

SimpleCoerciveRBEstimator estimate, restricted_to_subbasis
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
class pymor.reductors.coercive.SimpleCoerciveRBReductor(d, RB=None, orthogonal_projection=('initial_data', ), product=None, coercivity_estimator=None)[source]

Bases: pymor.reductors.basic.GenericRBReductor

Reductor for linear StationaryDiscretizations with affinely decomposed operator and rhs.

Note

The reductor CoerciveRBReductor can be used for arbitrary coercive StationaryDiscretizations and offers an improved error estimator with better numerical stability.

The only addition is to GenericRBReductor is an error estimator, which evaluates the norm of the residual with respect to a given inner product.

Parameters

d
The Discretization which is to be reduced.
RB
VectorArray containing the reduced basis on which to project.
orthogonal_projection
List of keys in d.operators for which the corresponding Operator should be orthogonally projected (i.e. operators which map to vectors in contrast to bilinear forms which map to functionals).
product
Inner product for the projection of the Operators given by orthogonal_projection and for the computation of Riesz representatives of the residual. If None, the Euclidean product is used.
coercivity_estimator
None or a ParameterFunctional returning a lower bound for the coercivity constant of the given problem. Note that the computed error estimate is only guaranteed to be an upper bound for the error when an appropriate coercivity estimate is specified.

Methods

SimpleCoerciveRBReductor reduce
GenericRBReductor extend_basis, reconstruct
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid

parabolic module

class pymor.reductors.parabolic.ParabolicRBEstimator(residual, residual_range_dims, initial_residual, initial_residual_range_dims, coercivity_estimator)[source]

Bases: pymor.core.interfaces.ImmutableInterface

Instantiated by ParabolicRBReductor.

Not to be used directly.

Methods

ParabolicRBEstimator estimate, restricted_to_subbasis
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
class pymor.reductors.parabolic.ParabolicRBReductor(d, RB=None, product=None, coercivity_estimator=None)[source]

Bases: pymor.reductors.basic.GenericRBReductor

Reduced Basis Reductor for parabolic equations.

This reductor uses GenericRBReductor for the actual RB-projection. The only addition is the assembly of an error estimator which bounds the discrete l2-in time / energy-in space error similar to [GP05], [HO08] as follows:

\left[ C_a^{-1}(\mu)\|e_N(\mu)\|^2 + \sum_{n=1}^{N} \Delta t\|e_n(\mu)\|^2_e \right]^{1/2} \leq \left[ C_a^{-1}(\mu)\Delta t \sum_{n=1}^{N}\|\mathcal{R}^n(u_n(\mu), \mu)\|^2_{e,-1} + C_a^{-1}(\mu)\|e_0\|^2 \right]^{1/2}

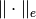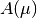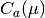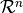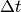Here, \|\cdot\| denotes the norm induced by the problem’s mass matrix (e.g. the L^2-norm) and \|\cdot\|_e is an arbitrary energy norm w.r.t. which the space operator A(\mu) is coercive, and C_a(\mu) is a lower bound for its coercivity constant. Finally, \mathcal{R}^n denotes the implicit Euler timestepping residual for the (fixed) time step size \Delta t,

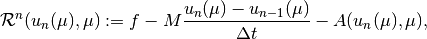
\mathcal{R}^n(u_n(\mu), \mu) := f - M \frac{u_{n}(\mu) - u_{n-1}(\mu)}{\Delta t} - A(u_n(\mu), \mu),

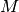where M denotes the mass operator and 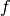f the source term. The dual norm of the residual is computed using the numerically stable projection from [BEOR14].

Warning

The reduced basis RB is required to be orthonormal w.r.t. the given energy product. If not, the projection of the initial values will be computed incorrectly.

[GP05]M. A. Grepl, A. T. Patera, A Posteriori Error Bounds For Reduced-Basis Approximations Of Parametrized Parabolic Partial Differential Equations, M2AN 39(1), 157-181, 2005.
[HO08]B. Haasdonk, M. Ohlberger, Reduced basis method for finite volume approximations of parametrized evolution equations, M2AN 42(2), 277-302, 2008.

Parameters

discretization
The InstationaryDiscretization which is to be reduced.
RB
VectorArray containing the reduced basis on which to project.
product
The energy inner product Operator w.r.t. the reduction error is estimated. RB must be to be orthonomrmal w.r.t. this product!
coercivity_estimator
None or a ParameterFunctional returning a lower bound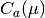 C_a(\mu) for the coercivity constant of discretization.operator w.r.t. product.

Methods

ParabolicRBReductor reduce
GenericRBReductor extend_basis, reconstruct
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid

residual module

class pymor.reductors.residual.ImplicitEulerResidualOperator(operator, mass, functional, dt, name=None)[source]

Bases: pymor.operators.basic.OperatorBase

Instantiated by ImplicitEulerResidualReductor.

Methods

ImplicitEulerResidualOperator apply, projected_to_subbasis
OperatorBase apply2, apply_inverse, apply_inverse_transpose, apply_transpose, as_range_array, as_source_array, assemble, jacobian, pairwise_apply2
OperatorInterface as_vector, assemble_lincomb, restricted
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors
Parametric build_parameter_type, parse_parameter, strip_parameter

Attributes

OperatorInterface linear, range, solver_options, source, T
ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
Parametric parameter_space, parameter_type, parametric
class pymor.reductors.residual.ImplicitEulerResidualReductor(RB, operator, mass, dt, functional=None, product=None)[source]

Bases: pymor.core.interfaces.BasicInterface

Reduced basis residual reductor with mass operator for implicit Euler timestepping.

Given an operator, mass and a functional, the concatenation of residual operator with the Riesz isomorphism is given by:

riesz_residual.apply(U, U_old, mu)
    == product.apply_inverse(operator.apply(U, mu) + 1/dt*mass.apply(U, mu) - 1/dt*mass.apply(U_old, mu)
       - functional.as_vector(mu))

This reductor determines a low-dimensional subspace of the image of a reduced basis space under riesz_residual using estimate_image_hierarchical, computes an orthonormal basis residual_range of this range space and then returns the Petrov-Galerkin projection

projected_riesz_residual
    === riesz_residual.projected(range_basis=residual_range, source_basis=RB)

of the riesz_residual operator. Given reduced basis coefficient vectors u and u_old, the dual norm of the residual can then be computed as

projected_riesz_residual.apply(u, u_old, mu).l2_norm()

Moreover, a reconstruct method is provided such that

residual_reductor.reconstruct(projected_riesz_residual.apply(u, u_old, mu))
    == riesz_residual.apply(RB.lincomb(u), RB.lincomb(u_old), mu)

Parameters

operator
See definition of riesz_residual.
mass
The mass operator. See definition of riesz_residual.
dt
The time step size. See definition of riesz_residual.
functional
See definition of riesz_residual. If None, zero right-hand side is assumed.
RB
VectorArray containing a basis of the reduced space onto which to project.
product
Inner product Operator w.r.t. which to compute the Riesz representatives.

Methods

ImplicitEulerResidualReductor reconstruct, reduce
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid
reconstruct(u)[source]

Reconstruct high-dimensional residual vector from reduced vector u.

class pymor.reductors.residual.NonProjectedImplicitEulerResidualOperator(operator, mass, functional, dt, product)[source]

Bases: pymor.reductors.residual.ImplicitEulerResidualOperator

Instantiated by ImplicitEulerResidualReductor.

Not to be used directly.

Methods

NonProjectedImplicitEulerResidualOperator apply, projected_to_subbasis
OperatorBase apply2, apply_inverse, apply_inverse_transpose, apply_transpose, as_range_array, as_source_array, assemble, jacobian, pairwise_apply2
OperatorInterface as_vector, assemble_lincomb, restricted
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors
Parametric build_parameter_type, parse_parameter, strip_parameter

Attributes

OperatorInterface linear, range, solver_options, source, T
ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
Parametric parameter_space, parameter_type, parametric
class pymor.reductors.residual.NonProjectedResidualOperator(operator, rhs, rhs_is_functional, product)[source]

Bases: pymor.reductors.residual.ResidualOperator

Instantiated by ResidualReductor.

Not to be used directly.

Methods

NonProjectedResidualOperator apply, projected_to_subbasis
OperatorBase apply2, apply_inverse, apply_inverse_transpose, apply_transpose, as_range_array, as_source_array, assemble, jacobian, pairwise_apply2
OperatorInterface as_vector, assemble_lincomb, restricted
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors
Parametric build_parameter_type, parse_parameter, strip_parameter

Attributes

OperatorInterface linear, range, solver_options, source, T
ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
Parametric parameter_space, parameter_type, parametric
class pymor.reductors.residual.ResidualOperator(operator, rhs, rhs_is_functional=True, name=None)[source]

Bases: pymor.operators.basic.OperatorBase

Instantiated by ResidualReductor.

Methods

ResidualOperator apply, projected_to_subbasis
OperatorBase apply2, apply_inverse, apply_inverse_transpose, apply_transpose, as_range_array, as_source_array, assemble, jacobian, pairwise_apply2
OperatorInterface as_vector, assemble_lincomb, restricted
ImmutableInterface generate_sid, with_, __setattr__
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors
Parametric build_parameter_type, parse_parameter, strip_parameter

Attributes

OperatorInterface linear, range, solver_options, source, T
ImmutableInterface add_with_arguments, sid, sid_ignore, with_arguments
BasicInterface logger, logging_disabled, name, uid
Parametric parameter_space, parameter_type, parametric
class pymor.reductors.residual.ResidualReductor(RB, operator, rhs=None, product=None)[source]

Bases: pymor.core.interfaces.BasicInterface

Generic reduced basis residual reductor.

Given an operator and a right-hand side, the residual is given by:

residual.apply(U, mu) == operator.apply(U, mu) - rhs.as_vector(mu)

When the rhs is a functional we are interested in the Riesz representative of the residual:

residual.apply(U, mu)
    == product.apply_inverse(operator.apply(U, mu) - rhs.as_vector(mu))

Given a basis RB of a subspace of the source space of operator, this reductor uses estimate_image_hierarchical to determine a low-dimensional subspace containing the image of the subspace under residual (resp. riesz_residual), computes an orthonormal basis residual_range for this range space and then returns the Petrov-Galerkin projection

projected_residual
    === project(residual, range_basis=residual_range, source_basis=RB)

of the residual operator. Given a reduced basis coefficient vector u, w.r.t. RB, the (dual) norm of the residual can then be computed as

projected_residual.apply(u, mu).l2_norm()

Moreover, a reconstruct method is provided such that

residual_reductor.reconstruct(projected_residual.apply(u, mu))
    == residual.apply(RB.lincomb(u), mu)

Parameters

RB
VectorArray containing a basis of the reduced space onto which to project.
operator
See definition of residual.
rhs
See definition of residual. If None, zero right-hand side is assumed.
product
Inner product Operator w.r.t. which to orthonormalize and w.r.t. which to compute the Riesz representatives in case rhs is a functional.

Methods

ResidualReductor reconstruct, reduce
BasicInterface disable_logging, enable_logging, has_interface_name, implementor_names, implementors

Attributes

BasicInterface logger, logging_disabled, name, uid
reconstruct(u)[source]

Reconstruct high-dimensional residual vector from reduced vector u.