pymor.algorithms package¶

Submodules¶

adaptivegreedy module¶

class pymor.algorithms.adaptivegreedy.AdaptiveSampleSet(parameter_space)[source]¶

Bases: pymor.core.interfaces.BasicInterface

An adaptive parameter sample set.

Used by adaptive_greedy.

Methods

`AdaptiveSampleSet`	`map_vertex_to_mu`, `refine`, `visualize`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`AdaptiveSampleSet`	`Element`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

pymor.algorithms.adaptivegreedy._estimate(mu, rd=None, d=None, reductor=None, error_norm=None)[source]¶: Called by adaptive_greedy.

pymor.algorithms.adaptivegreedy.adaptive_greedy(discretization, reductor, parameter_space=None, use_estimator=True, error_norm=None, target_error=None, max_extensions=None, validation_mus=0, rho=1.1, gamma=0.2, theta=0.0, extension_params=None, visualize=False, visualize_vertex_size=80, pool=<pymor.parallel.dummy.DummyPool object>)[source]¶

Greedy basis generation algorithm with adaptively refined training set.

This method extends pyMOR’s default greedy greedy basis generation algorithm by adaptive refinement of the parameter training set according to [HDO11] to prevent overfitting of the reduced basis to the training set. This is achieved by estimating the reduction error on an additional validation set of parameters. If the ratio between the estimated errors on the validation set and the validation set is larger than rho, the training set is refined using standard grid refinement techniques.

[HDO11]

Haasdonk, B.; Dihlmann, M. & Ohlberger, M., A training set and multiple bases generation approach for parameterized model reduction based on adaptive grids in parameter space, Math. Comput. Model. Dyn. Syst., 2011, 17, 423-442

Parameters

discretization

See greedy.

reductor

See greedy.

parameter_space

The ParameterSpace for which to compute the reduced model. If None, the parameter space of the discretization is used.

use_estimator

See greedy.

error_norm

See greedy.

target_error

See greedy.

max_extensions

See greedy.

validation_mus

One of the following:

a list of Parameters to use as validation set,
a positive number indicating the number of random parameters to use as validation set,
a non-positive number, indicating the negative number of random parameters to use as validation set in addition to the centers of the elements of the adaptive training set.

rho

Maximum allowed ratio between maximum estimated error on validation set vs. maximum estimated error on training set. If the ratio is larger, the training set is refined.

gamma

Weight of the age penalty term in the training set refinement indicators.

theta

Ratio of training set elements to select for refinement. (One element is always refined.)

extension_params

See greedy.

visualize

If True, visualize the refinement indicators. (Only available for 2 and 3 dimensional parameter spaces.)

visualize_vertex_size

Size of the vertices in the visualization.

pool

See greedy.

Returns

Dict with the following fields

reduced_discretization: The reduced Discretization obtained for the computed basis.

extensions: Number of greedy iterations.

max_errs: Sequence of maximum errors during the greedy run.

max_err_mus: The parameters corresponding to max_errs.

max_val_errs: Sequence of maximum errors on the validation set.

max_val_err_mus: The parameters corresponding to max_val_errs.

refinements: Number of refinements made in each extension step.

training_set_sizes: The final size of the training set in each extension step.

time: Duration of the algorithm.

reduction_data: Reduction data returned by the last reductor call.

basic module¶

Module containing some basic but generic linear algebra algorithms.

pymor.algorithms.basic.almost_equal(U, V, product=None, norm=None, rtol=1e-14, atol=1e-14)[source]¶

Compare U and V for almost equality.

The vectors of U and V are compared in pairs for almost equality. Two vectors u and v are considered almost equal iff

||u - v|| <= atol + ||v|| * rtol.

The norm to be used can be specified via the norm or product parameter.

If the length of U resp. V is 1, the single specified vector is compared to all vectors of the other array. Otherwise, the lengths of both indexed arrays have to agree.

Parameters

U, V: VectorArrays to be compared.
product: If specified, use this inner product Operator to compute the norm. product and norm are mutually exclusive.
norm: If specified, must be a callable, which is used to compute the norm or, alternatively, one of the string ‘l1’, ‘l2’, ‘sup’, in which case the respective VectorArray norm methods are used. product and norm are mutually exclusive. If neither is specified, norm='l2' is assumed.
rtol: The relative tolerance.
atol: The absolute tolerance.

Defaults

rtol, atol (see pymor.core.defaults)

ei module¶

This module contains algorithms for the empirical interpolation of Operators.

The main work for generating the necessary interpolation data is handled by the ei_greedy method. The objects returned by this method can be used to instantiate an EmpiricalInterpolatedOperator.

As a convenience, the interpolate_operators method allows to perform the empirical interpolation of the Operators of a given discretization with a single function call.

pymor.algorithms.ei.deim(U, modes=None, error_norm=None, product=None)[source]¶

Generate data for empirical interpolation using DEIM algorithm.

Given a VectorArray U, this method generates a collateral basis and interpolation DOFs for empirical interpolation of the vectors contained in U. The returned objects can be used to instantiate an EmpiricalInterpolatedOperator (with triangular=False).

The collateral basis is determined by the first pod modes of U.

Parameters

U: A VectorArray of vectors to interpolate.
modes: Dimension of the collateral basis i.e. number of POD modes of the vectors in U.
error_norm: Norm w.r.t. which to calculate the interpolation error. If None, the Euclidean norm is used.
product: Inner product Operator used for the POD.

Returns

interpolation_dofs

NumPy array of the DOFs at which the vectors are interpolated.

collateral_basis

VectorArray containing the generated collateral basis.

data

Dict containing the following fields:

errors: Sequence of maximum approximation errors during greedy search.

pymor.algorithms.ei.ei_greedy(U, error_norm=None, atol=None, rtol=None, max_interpolation_dofs=None, copy=True, pool=<pymor.parallel.dummy.DummyPool object>)[source]¶

Generate data for empirical interpolation using EI-Greedy algorithm.

Given a VectorArray U, this method generates a collateral basis and interpolation DOFs for empirical interpolation of the vectors contained in U. The returned objects can be used to instantiate an EmpiricalInterpolatedOperator (with triangular=True).

The interpolation data is generated by a greedy search algorithm, where in each loop iteration the worst approximated vector in U is added to the collateral basis.

Parameters

U: A VectorArray of vectors to interpolate.
error_norm: Norm w.r.t. which to calculate the interpolation error. If None, the Euclidean norm is used.
atol: Stop the greedy search if the largest approximation error is below this threshold.
rtol: Stop the greedy search if the largest relative approximation error is below this threshold.
max_interpolation_dofs: Stop the greedy search if the number of interpolation DOF (= dimension of the collateral basis) reaches this value.
copy: If False, U will be modified during executing of the algorithm.
pool: If not None, the WorkerPool to use for parallelization.

Returns

interpolation_dofs

NumPy array of the DOFs at which the vectors are evaluated.

collateral_basis

VectorArray containing the generated collateral basis.

data

Dict containing the following fields:

errors: Sequence of maximum approximation errors during greedy search.

triangularity_errors: Sequence of maximum absolute values of interoplation matrix coefficients in the upper triangle (should be near zero).

pymor.algorithms.ei.interpolate_operators(discretization, operator_names, parameter_sample, error_norm=None, atol=None, rtol=None, max_interpolation_dofs=None, pool=<pymor.parallel.dummy.DummyPool object>)[source]¶

Empirical operator interpolation using the EI-Greedy algorithm.

This is a convenience method to facilitate the use of ei_greedy. Given a Discretization, names of Operators, and a sample of Parameters, first the operators are evaluated on the solution snapshots of the discretization for the provided parameters. These evaluations are then used as input for ei_greedy. Finally the resulting interpolation data is used to create EmpiricalInterpolatedOperators and a new discretization with the interpolated operators is returned.

Note that this implementation creates one common collateral basis for all specified operators, which might not be what you want.

Parameters

discretization: The Discretization whose Operators will be interpolated.
operator_names: List of keys in the operators dict of the discretization. The corresponding Operators will be interpolated.
parameter_sample: A list of Parameters for which solution snapshots are calculated.
error_norm: See ei_greedy.
atol: See ei_greedy.
rtol: See ei_greedy.
max_interpolation_dofs: See ei_greedy.
pool: If not None, the WorkerPool to use for parallelization.

Returns

ei_discretization

Discretization with Operators given by operator_names replaced by EmpiricalInterpolatedOperators.

data

Dict containing the following fields:

dofs: NumPy array of the DOFs at which the Operators have to be evaluated.

basis: VectorArray containing the generated collateral basis.

errors: Sequence of maximum approximation errors during greedy search.

triangularity_errors: Sequence of maximum absolute values of interoplation matrix coefficients in the upper triangle (should be near zero).

error module¶

pymor.algorithms.error.reduction_error_analysis(reduced_discretization, discretization=None, reductor=None, test_mus=10, basis_sizes=0, random_seed=None, estimator=True, condition=False, error_norms=(), error_norm_names=None, estimator_norm_index=0, custom=(), plot=False, plot_custom_logarithmic=True, pool=<pymor.parallel.dummy.DummyPool object>)[source]¶

Analyze the model reduction error.

The maximum model reduction error is estimated by solving the reduced Discretization for given random Parameters.

Parameters

reduced_discretization

The reduced Discretization.

discretization

The high-dimensional Discretization. Must be specified if error_norms are given.

reductor

The reductor which has created reduced_discretization. Must be specified if error_norms are given.

test_mus

Either a list of Parameters to compute the errors for, or the number of parameters which are sampled randomly from parameter_space (if given) or reduced_discretization.parameter_space.

basis_sizes

Either a list of reduced basis dimensions to consider, or the number of dimensions (which are then selected equidistantly, always including the maximum reduced space dimension). The dimensions are input for ~pymor.reductors.basic.reduce_to_subbasis to quickly obtain smaller reduced Discretizations from rb_discretization.

random_seed

If test_mus is a number, use this value as random seed for drawing the Parameters.

estimator

If True evaluate the error estimator of reduced_discretization on the test Parameters.

condition

If True, compute the condition of the reduced system matrix for the given test Parameters (can only be specified if rb_discretization is an instance of StationaryDiscretization and rb_discretization.operator is linear).

error_norms

List of norms in which to compute the model reduction error.

error_norm_names

Names of the norms given by error_norms. If None, the name attributes of the given norms are used.

estimator_norm_index

When estimator is True and error_norms are specified, this is the index of the norm in error_norms w.r.t. which to compute the effectivity of the estimator.

custom

List of custom functions which are evaluated for each test Parameter and basis size. The functions must have the signature

def custom_value(reduced_discretization, discretization=d,
                 reductor, mu, dim):
    pass

plot

If True, generate a plot of the computed quantities w.r.t. the basis size.

plot_custom_logarithmic

If True, use a logarithmic y-axis to plot the computed custom values.

pool

If not None, the WorkerPool to use for parallelization.

Returns

Dict with the following fields

mus: The test Parameters which have been considered.

basis_sizes: The reduced basis dimensions which have been considered.

norms: NumPy array of the norms of the high-dimensional solutions w.r.t. all given test Parameters, reduced basis dimensions and norms in error_norms. (Only present when error_norms has been specified.)

max_norms: Maxima of norms over the given test Parameters.

max_norm_mus: Parameters corresponding to max_norms.

errors: NumPy array of the norms of the model reduction errors w.r.t. all given test Parameters, reduced basis dimensions and norms in error_norms. (Only present when error_norms has been specified.)

max_errors: Maxima of errors over the given test Parameters.

max_error_mus: Parameters corresponding to max_errors.

rel_errors: errors divided by norms. (Only present when error_norms has been specified.)

max_rel_errors: Maxima of rel_errors over the given test Parameters.

max_rel_error_mus: Parameters corresponding to max_rel_errors.

error_norm_names: Names of the given error_norms. (Only present when error_norms has been specified.)

estimates: NumPy array of the model reduction error estimates w.r.t. all given test Parameters and reduced basis dimensions. (Only present when estimator is True.)

max_estimate: Maxima of estimates over the given test Parameters.

max_estimate_mus: Parameters corresponding to max_estimates.

effectivities: errors divided by estimates. (Only present when estimator is True and error_norms has been specified.)

min_effectivities: Minima of effectivities over the given test Parameters.

min_effectivity_mus: Parameters corresponding to min_effectivities.

max_effectivities: Maxima of effectivities over the given test Parameters.

max_effectivity_mus: Parameters corresponding to max_effectivities.

errors: NumPy array of the reduced system matrix conditions w.r.t. all given test Parameters and reduced basis dimensions. (Only present when conditions is True.)

max_conditions: Maxima of conditions over the given test Parameters.

max_condition_mus: Parameters corresponding to max_conditions.

custom_values: NumPy array of custom function evaluations w.r.t. all given test Parameters, reduced basis dimensions and functions in custom. (Only present when custom has been specified.)

max_custom_values: Maxima of custom_values over the given test Parameters.

max_custom_values_mus: Parameters corresponding to max_custom_values.

time: Time (in seconds) needed for the error analysis.

summary: String containing a summary of all computed quantities for the largest (last) considered basis size.

figure: The figure containing the generated plots. (Only present when plot is True.)

genericsolvers module¶

This module contains some iterative linear solvers which only use the Operator interface

pymor.algorithms.genericsolvers.apply_inverse(op, rhs, options=None, least_squares=False, check_finite=True, default_solver='generic_lgmres', default_least_squares_solver='generic_least_squares_lsmr')[source]¶

Solve linear equation system.

Applies the inverse of op to the vectors in rhs using a generic iterative solver.

Parameters

op: The linear, non-parametric Operator to invert.
rhs: VectorArray of right-hand sides for the equation system.
options: The solver_options to use (see solver_options).
check_finite: Test if solution only containes finite values.
default_solver: Default solver to use (generic_lgmres, generic_least_squares_lsmr, generic_least_squares_lsqr).
default_least_squares_solver: Default solver to use for least squares problems (generic_least_squares_lsmr, generic_least_squares_lsqr).

Returns

VectorArray of the solution vectors.

Defaults

check_finite, default_solver, default_least_squares_solver (see pymor.core.defaults)

pymor.algorithms.genericsolvers.lgmres(A, b, x0=None, tol=1e-05, maxiter=1000, M=None, callback=None, inner_m=30, outer_k=3, outer_v=None, store_outer_Av=True)[source]¶

pymor.algorithms.genericsolvers.lsmr(A, b, damp=0.0, atol=1e-06, btol=1e-06, conlim=100000000.0, maxiter=None, show=False)[source]¶

pymor.algorithms.genericsolvers.lsqr(A, b, damp=0.0, atol=1e-08, btol=1e-08, conlim=100000000.0, iter_lim=None, show=False)[source]¶

pymor.algorithms.genericsolvers.solver_options(lgmres_tol=1e-05, lgmres_maxiter=1000, lgmres_inner_m=39, lgmres_outer_k=3, least_squares_lsmr_damp=0.0, least_squares_lsmr_atol=1e-06, least_squares_lsmr_btol=1e-06, least_squares_lsmr_conlim=100000000.0, least_squares_lsmr_maxiter=None, least_squares_lsmr_show=False, least_squares_lsqr_damp=0.0, least_squares_lsqr_atol=1e-06, least_squares_lsqr_btol=1e-06, least_squares_lsqr_conlim=100000000.0, least_squares_lsqr_iter_lim=None, least_squares_lsqr_show=False)[source]¶

Returns available solvers with default solver_options.

Parameters

lgmres_tol: See scipy.sparse.linalg.lgmres.
lgmres_maxiter: See scipy.sparse.linalg.lgmres.
lgmres_inner_m: See scipy.sparse.linalg.lgmres.
lgmres_outer_k: See scipy.sparse.linalg.lgmres.
least_squares_lsmr_damp: See scipy.sparse.linalg.lsmr.
least_squares_lsmr_atol: See scipy.sparse.linalg.lsmr.
least_squares_lsmr_btol: See scipy.sparse.linalg.lsmr.
least_squares_lsmr_conlim: See scipy.sparse.linalg.lsmr.
least_squares_lsmr_maxiter: See scipy.sparse.linalg.lsmr.
least_squares_lsmr_show: See scipy.sparse.linalg.lsmr.
least_squares_lsqr_damp: See scipy.sparse.linalg.lsqr.
least_squares_lsqr_atol: See scipy.sparse.linalg.lsqr.
least_squares_lsqr_btol: See scipy.sparse.linalg.lsqr.
least_squares_lsqr_conlim: See scipy.sparse.linalg.lsqr.
least_squares_lsqr_iter_lim: See scipy.sparse.linalg.lsqr.
least_squares_lsqr_show: See scipy.sparse.linalg.lsqr.

Returns

A dict of available solvers with default solver_options.

Defaults

lgmres_tol, lgmres_maxiter, lgmres_inner_m, lgmres_outer_k, least_squares_lsmr_damp, least_squares_lsmr_atol, least_squares_lsmr_btol, least_squares_lsmr_conlim, least_squares_lsmr_maxiter, least_squares_lsmr_show, least_squares_lsqr_atol, least_squares_lsqr_btol, least_squares_lsqr_conlim, least_squares_lsqr_iter_lim, least_squares_lsqr_show (see pymor.core.defaults)

gram_schmidt module¶

pymor.algorithms.gram_schmidt.gram_schmidt(A, product=None, atol=1e-13, rtol=1e-13, offset=0, find_duplicates=True, reiterate=True, reiteration_threshold=0.1, check=True, check_tol=0.001, copy=True)[source]¶

Orthonormalize a VectorArray using the stabilized Gram-Schmidt algorithm.

Parameters

A: The VectorArray which is to be orthonormalized.
product: The inner product Operator w.r.t. which to orthonormalize. If None, the Euclidean product is used.
atol: Vectors of norm smaller than atol are removed from the array.
rtol: Relative tolerance used to detect linear dependent vectors (which are then removed from the array).
offset: Assume that the first offset vectors are already orthonormal and start the algorithm at the offset + 1-th vector.
reiterate: If True, orthonormalize again if the norm of the orthogonalized vector is much smaller than the norm of the original vector.
reiteration_threshold: If reiterate is True, re-orthonormalize if the ratio between the norms of the orthogonalized vector and the original vector is smaller than this value.
check: If True, check if the resulting VectorArray is really orthonormal.
check_tol: Tolerance for the check.
copy: If True, create a copy of A instead of modifying A in-place.
find_duplicates: unused

Returns

The orthonormalized VectorArray.

Defaults

atol, rtol, reiterate, reiteration_threshold, check, check_tol (see pymor.core.defaults)

pymor.algorithms.gram_schmidt.gram_schmidt_biorth(V, W, product=None, reiterate=True, reiteration_threshold=0.1, check=True, check_tol=0.001, copy=True)[source]¶

Biorthonormalize a pair of VectorArrays using the biorthonormal Gram-Schmidt process.

See Algorithm 1 in [BKS11].

[BKS11]

P. Benner, M. Köhler, J. Saak, Sparse-Dense Sylvester Equations in 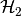$\mathcal{H}_2$ -Model Order Reduction, Max Planck Institute Magdeburg Preprint, available from http://www.mpi-magdeburg.mpg.de/preprints/, 2011.

Parameters

V, W: The VectorArrays which are to be biorthonormalized.
product: The inner product Operator w.r.t. which to biorthonormalize. If None, the Euclidean product is used.
reiterate: If True, orthonormalize again if the norm of the orthogonalized vector is much smaller than the norm of the original vector.
reiteration_threshold: If reiterate is True, re-orthonormalize if the ratio between the norms of the orthogonalized vector and the original vector is smaller than this value.
check: If True, check if the resulting VectorArray is really orthonormal.
check_tol: Tolerance for the check.
copy: If True, create a copy of V and W instead of modifying V and W in-place.

Returns

The biorthonormalized VectorArrays.

greedy module¶

pymor.algorithms.greedy.greedy(discretization, reductor, samples, use_estimator=True, error_norm=None, atol=None, rtol=None, max_extensions=None, extension_params=None, pool=None)[source]¶

Greedy basis generation algorithm.

This algorithm generates a reduced basis by iteratively adding the worst approximated solution snapshot for a given training set to the reduced basis. The approximation error is computed either by directly comparing the reduced solution to the detailed solution or by using an error estimator (use_estimator == True). The reduction and basis extension steps are performed by calling the methods provided by the reductor and extension_algorithm arguments.

Parameters

discretization: The Discretization to reduce.
reductor: Reductor for reducing the given Discretization. This has to be a an object with a reduce method, such that reductor.reduce() yields the reduced discretization, and an exted_basis method, such that reductor.extend_basis(U, copy_U=False, **extension_params) extends the current reduced basis by the vectors contained in U. For an example see CoerciveRBReductor.
samples: The set of Parameter samples on which to perform the greedy search.
use_estimator: If True, use reduced_discretization.estimate() to estimate the errors on the sample set. Otherwise discretization.solve() is called to compute the exact model reduction error.
error_norm: If use_estimator == False, use this function to calculate the norm of the error. If None, the Euclidean norm is used.
atol: If not None, stop the algorithm if the maximum (estimated) error on the sample set drops below this value.
rtol: If not None, stop the algorithm if the maximum (estimated) relative error on the sample set drops below this value.
max_extensions: If not None, stop the algorithm after max_extensions extension steps.
extension_params: dict of parameters passed to the reductor.extend_basis method.
pool: If not None, the WorkerPool to use for parallelization.

Returns

Dict with the following fields

reduced_discretization: The reduced Discretization obtained for the computed basis.

max_errs: Sequence of maximum errors during the greedy run.

max_err_mus: The parameters corresponding to max_errs.

extensions: Number of performed basis extensions.

time: Total runtime of the algorithm.

reduction_data: The reduction_data returned by the last reductor call.

image module¶

class pymor.algorithms.image.CollectOperatorRangeRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

RuleTable for the estimate_image algorithm.

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`CollectOperatorRangeRules`	`action_apply_operator`, `action_Concatenation`, `action_EmpiricalInterpolatedOperator`, `action_recurse`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

class pymor.algorithms.image.CollectVectorRangeRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

RuleTable for the estimate_image algorithm.

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`CollectVectorRangeRules`	`action_as_range_array`, `action_recurse`, `action_VectorArray`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

pymor.algorithms.image.estimate_image(operators=(), vectors=(), domain=None, extends=False, orthonormalize=True, product=None, riesz_representatives=False)[source]¶

Estimate the image of given Operators for all mu.

Let operators be a list of Operators with common source and range, and let vectors be a list of VectorArrays or vector-like Operators in the range of these operators. Given a VectorArray domain of vectors in the source of the operators, this algorithms determines a VectorArray image of range vectors such that the linear span of image contains:

op.apply(U, mu=mu) for all operators op in operators, for all possible Parameters mu and for all VectorArrays U contained in the linear span of domain,
U for all VectorArrays in vectors,
v.as_range_array(mu) for all Operators in vectors and all possible Parameters mu.

The algorithm will try to choose image as small as possible. However, no optimality is guaranteed. The image estimation algorithm is specified by CollectOperatorRangeRules and CollectVectorRangeRules.

Parameters

operators: See above.
vectors: See above.
domain: See above. If None, an empty domain VectorArray is assumed.
extends: For some operators, e.g. EmpiricalInterpolatedOperator, as well as for all elements of vectors, image is estimated independently from the choice of domain. If extends is True, such operators are ignored. (This is useful in case these vectors have already been obtained by earlier calls to this function.)
orthonormalize: Compute an orthonormal basis for the linear span of image using the gram_schmidt algorithm.
product: Inner product Operator w.r.t. which to orthonormalize.
riesz_representatives: If True, compute Riesz representatives of the vectors in image before orthonormalizing (useful for dual norm computation when the range of the operators is a dual space).

Returns

The VectorArray image.

Raises

ImageCollectionError: Is raised when for a given Operator no image estimate is possible.

pymor.algorithms.image.estimate_image_hierarchical(operators=(), vectors=(), domain=None, extends=None, orthonormalize=True, product=None, riesz_representatives=False)[source]¶

Estimate the image of given Operators for all mu.

This is an extended version of estimate_image, which calls estimate_image individually for each vector of domain.

As a result, the vectors in the returned image VectorArray will be ordered by the domain vector they correspond to (starting with vectors which correspond to the functionals and to Operators for which the image is estimated independently from domain).

This function also returns an image_dims list, such that the first image_dims[i+1] vectors of image correspond to the first i vectors of domain (the first image_dims[0] vectors correspond to vectors and to Operators with fixed image estimate).

Parameters

operators: See estimate_image.
vectors: See estimate_image.
domain: See estimate_image.
extends: When additional vectors have been appended to the domain VectorArray after estimate_image_hierarchical has been called, and estimate_image_hierarchical shall be called again for the extended domain array, extends can be set to (image, image_dims), where image, image_dims are the return values of the last estimate_image_hierarchical call. The old domain vectors will then be skipped during computation and image, image_dims will be modified in-place.
orthonormalize: See estimate_image.
product: See estimate_image.
riesz_representatives: See estimate_image.

Returns

image: See above.
image_dims: See above.

Raises

ImageCollectionError: Is raised when for a given Operator no image estimate is possible.

newton module¶

pymor.algorithms.newton.newton(operator, rhs, initial_guess=None, mu=None, error_norm=None, least_squares=False, miniter=0, maxiter=100, rtol=-1.0, atol=-1.0, stagnation_window=3, stagnation_threshold=0.9, return_stages=False, return_residuals=False)[source]¶

Basic Newton algorithm.

This method solves the nonlinear equation

A(U, mu) = V

for U using the Newton method.

Parameters

operator: The Operator A. A must implement the jacobian interface method.
rhs: VectorArray of length 1 containing the vector V.
initial_guess: If None, a VectorArray of length 1 containing an initial guess for the solution U.
mu: The Parameter for which to solve the equation.
error_norm: The norm with which the norm of the residual is computed. If None, the Euclidean norm is used.
least_squares: If True, use a least squares linear solver (e.g. for residual minimization).
miniter: Minimum amount of iterations to perform.
maxiter: Fail if the iteration count reaches this value without converging.
rtol: Finish when the residual norm has been reduced by this factor relative to the norm of the initial residual.
atol: Finish when the residual norm is below this threshold.
stagnation_window: Finish when the residual norm has not been reduced by a factor of stagnation_threshold during the last stagnation_window iterations.
stagnation_threshold: See stagnation_window.
return_stages: If True, return a VectorArray of the intermediate approximations of U after each iteration.
return_residuals: If True, return a VectorArray of all residual vectors which have been computed during the Newton iterations.

Returns

U

VectorArray of length 1 containing the computed solution

data

Dict containing the following fields:

error_sequence: NumPy array containing the residual norms after each iteration.

stages: See return_stages.

residuals: See return_residuals.

Raises

NewtonError: Raised if the Netwon algorithm failed to converge.

Defaults

miniter, maxiter, rtol, atol, stagnation_window, stagnation_threshold (see pymor.core.defaults)

pod module¶

pymor.algorithms.pod.pod(A, modes=None, product=None, rtol=4e-08, atol=0.0, l2_err=0.0, symmetrize=False, orthonormalize=True, check=True, check_tol=1e-10)[source]¶

Proper orthogonal decomposition of A.

Viewing the VectorArray A as a A.dim x len(A) matrix, the return value of this method is the VectorArray of left-singular vectors of the singular value decomposition of A, where the inner product on R^(dim(A)) is given by product and the inner product on R^(len(A)) is the Euclidean inner product.

Parameters

A

The VectorArray for which the POD is to be computed.

modes

If not None, only the first modes POD modes (singular vectors) are returned.

product

Inner product Operator w.r.t. which the POD is computed.

rtol

Singular values smaller than this value multiplied by the largest singular value are ignored.

atol

Singular values smaller than this value are ignored.

l2_err

Do not return more modes than needed to bound the l2-approximation error by this value. I.e. the number of returned modes is at most

argmin_N { sum_{n=N+1}^{infty} s_n^2 <= l2_err^2 }

where s_n denotes the n-th singular value.

symmetrize

If True, symmetrize the Gramian again before proceeding.

orthonormalize

If True, orthonormalize the computed POD modes again using the gram_schmidt algorithm.

check

If True, check the computed POD modes for orthonormality.

check_tol

Tolerance for the orthonormality check.

Returns

POD: VectorArray of POD modes.
SVALS: Sequence of singular values.

Defaults

rtol, atol, l2_err, symmetrize, orthonormalize, check, check_tol (see pymor.core.defaults)

preassemble module¶

class pymor.algorithms.preassemble.PreAssembleRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`PreAssembleRules`	`action_AdjointOperator`, `action_assemble`, `action_identity`, `action_recurse`, `action_recurse_and_assemble`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

pymor.algorithms.preassemble.preassemble(obj)[source]¶

projection module¶

class pymor.algorithms.projection.ProjectRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

RuleTable for the project algorithm.

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ProjectRules`	`action_AdjointOperator`, `action_AffineOperator`, `action_apply_basis`, `action_Concatenation`, `action_ConstantOperator`, `action_EmpiricalInterpolatedOperator`, `action_generic_projection`, `action_recurse`, `action_ZeroOperator`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

class pymor.algorithms.projection.ProjectToSubbasisRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

RuleTable for the project_to_subbasis algorithm.

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ProjectToSubbasisRules`	`action_ConstantOperator`, `action_NumpyMatrixOperator`, `action_ProjectedEmpiciralInterpolatedOperator`, `action_ProjectedOperator`, `action_recurse`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

pymor.algorithms.projection.project(op, range_basis, source_basis, product=None)[source]¶

Petrov-Galerkin projection of a given Operator.

Given an inner product ( ⋅, ⋅), source vectors b_1, ..., b_N and range vectors c_1, ..., c_M, the projection op_proj of op is defined by

[ op_proj(e_j) ]_i = ( c_i, op(b_j) )

for all i,j, where e_j denotes the j-th canonical basis vector of R^N.

In particular, if the c_i are orthonormal w.r.t. the given product, then op_proj is the coordinate representation w.r.t. the b_i/c_i bases of the restriction of op to span(b_i) concatenated with the orthogonal projection onto span(c_i).

From another point of view, if op is viewed as a bilinear form (see apply2) and ( ⋅, ⋅ ) is the Euclidean inner product, then op_proj represents the matrix of the bilinear form restricted to span(b_i) / span(c_i) (w.r.t. the b_i/c_i bases).

How the projection is realized will depend on the given Operator. While a projected NumpyMatrixOperator will again be a NumpyMatrixOperator, only a generic ProjectedOperator can be returned in general. The exact algorithm is specified in ProjectRules.

Parameters

range_basis: The vectors c_1, ..., c_M as a VectorArray. If None, no projection in the range space is performed.
source_basis: The vectors b_1, ..., b_N as a VectorArray or None. If None, no restriction of the source space is performed.
product: An Operator representing the inner product. If None, the Euclidean inner product is chosen.

Returns

The projected Operator op_proj.

pymor.algorithms.projection.project_to_subbasis(op, dim_range=None, dim_source=None)[source]¶

Project given already projected Operator to a subbasis.

The purpose of this method is to further project an operator that has been obtained through project to subbases of the original projection bases, i.e.

project_to_subbasis(project(op, r_basis, s_basis, prod), dim_range, dim_source)

should be the same as

project(op, r_basis[:dim_range], s_basis[:dim_source], prod)

For a NumpyMatrixOperator this amounts to extracting the upper-left (dim_range, dim_source) corner of its matrix.

The subbasis projection algorithm is specified in ProjectToSubbasisRules.

Parameters

dim_range: Dimension of the range subbasis.
dim_source: Dimension of the source subbasis.

Returns

The projected Operator.

rules module¶

class pymor.algorithms.rules.RuleTable[source]¶

Bases: pymor.core.interfaces.BasicInterface

Define algorithm by a table of match conditions and corresponding actions.

RuleTable manages a table of rules, stored in the rules attributes, which can be applied to given objects.

A new table is created by subclassing RuleTable and defining new methods which are decorated with match_class, match_generic or another rule subclass. The order of the method definitions determines the order in which the defined rules are applied.

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`RuleTable`	`rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

rules¶: list of all defined rules.

apply(obj, *args, **kwargs)[source]¶

Sequentially apply rules to given object.

This method iterates over all rules of the given RuleTable. For each rule, it is checked if it matches the given object. If False, the next rule in the table is considered. If True the corresponding action is executed with obj, *args and **kwargs as parameters. If execution of action raises RuleNotMatchingError, the rule is considered as not matching, and execution continues with evaluation of the next rule. Otherwise, execution is stopped and the return value of rule.action is returned to the caller.

If no rule matches, a NoMatchingRuleError is raised.

Parameters

obj: The object to apply the RuleTable to.
args: Positional arguments for the action.
kwargs: Keyword arguments for the action.

Returns

Return value of the action of the first matching rule in the table.

Raises

NoMatchingRuleError: No rule could be applied to the given object.

apply_children(obj, *args, *, children=None, **kwargs)[source]¶

Apply rules to all children of the given object.

This method calls apply to each child of the given object. The children of the object are either provided by the children parameter or authomatically infered by the get_children method.

Parameters

obj: The object to apply the RuleTable to.
args: Positional arguments for the action.
children: None or a list of attribute names defining the children to consider.
kwargs: Keyword arguments for the action.

Returns

Result of : meth:apply for all given children.

classmethod get_children(obj)[source]¶

Determine children of given object.

This method returns a list of the names of all attributes a, for which one of the folling is true:

a is an Operator.

a is a mapping and each of its values is either an Operator or None.

a is an iterable and each of its elements is either an Operator or None.

replace_children(obj, *args, *, children=None, **kwargs)[source]¶

Replace children of object according to rule table.

Same as apply_children, but additionally calls obj.with_ to replace the children of obj with the result of the corresponding apply call.

class pymor.algorithms.rules.RuleTableMeta(name, bases, namespace)[source]¶

Bases: pymor.core.interfaces.UberMeta

Meta class for RuleTable.

Methods

`ABCMeta`	`register`, `__instancecheck__`, `__subclasscheck__`
`type`	`mro`, `__dir__`, `__prepare__`, `__sizeof__`, `__subclasses__`

class pymor.algorithms.rules.match_class(*classes)[source]¶

Bases: pymor.algorithms.rules.rule

rule that matches when obj is instance of one of the given classes.

Methods

match_class

matches

Attributes

`match_class`	`condition_type`
`rule`	`action`, `action_description`, `condition_description`, `source`

class pymor.algorithms.rules.match_generic(condition, condition_description=None)[source]¶

Bases: pymor.algorithms.rules.rule

rule with matching condition given by an arbitrary function.

Parameters

condition: Function of one argument which checks if given object matches condition.
condition_description: Optional string describing the condition implemented by condition.

Methods

match_generic

matches

Attributes

`match_generic`	`condition_type`
`rule`	`action`, `action_description`, `condition_description`, `source`

pymor.algorithms.rules.print_children(obj)[source]¶

class pymor.algorithms.rules.rule[source]¶

Bases: object

Decorator to make a method a rule in a given RuleTable.

The decorated function will become the action to perform in case the rule matches. Matching conditions are specified by subclassing and overriding the matches method.

Methods

rule

matches

Attributes

rule action, action_description, condition_description, condition_type, source

action¶: Method to call in case the rule matches.

matches(obj)[source]¶: Returns True if given object matches the condition.

timestepping module¶

This module provides generic time-stepping algorithms for the solution of instationary problems.

The algorithms are generic in the sense that each algorithms operates exclusively on Operators and VectorArrays. In particular, the algorithms can also be used to turn an arbitrary stationary Discretization provided by an external library into an instationary Discretization.

Currently, implementations of explicit_euler and implicit_euler time-stepping are provided. The TimeStepperInterface defines a common interface that has to be fulfilled by the time-steppers used by InstationaryDiscretization. The classes ExplicitEulerTimeStepper and ImplicitEulerTimeStepper encapsulate explicit_euler and implicit_euler to provide this interface.

class pymor.algorithms.timestepping.ExplicitEulerTimeStepper(nt)[source]¶

Bases: pymor.algorithms.timestepping.TimeStepperInterface

Explicit Euler time-stepper.

Solves equations of the form

M * d_t u + A(u, mu, t) = F(mu, t).

Parameters

nt: The number of time-steps the time-stepper will perform.

Methods

`ExplicitEulerTimeStepper`	`solve`
`ImmutableInterface`	`generate_sid`, `with_`, `__setattr__`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ImmutableInterface`	`add_with_arguments`, `sid`, `sid_ignore`, `with_arguments`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

class pymor.algorithms.timestepping.ImplicitEulerTimeStepper(nt, solver_options='operator')[source]¶

Bases: pymor.algorithms.timestepping.TimeStepperInterface

Implict Euler time-stepper.

Solves equations of the form

M * d_t u + A(u, mu, t) = F(mu, t).

Parameters

nt: The number of time-steps the time-stepper will perform.
solver_options: The solver_options used to invert M + dt*A. The special values 'mass' and 'operator' are recognized, in which case the solver_options of M (resp. A) are used.

Methods

`ImplicitEulerTimeStepper`	`solve`
`ImmutableInterface`	`generate_sid`, `with_`, `__setattr__`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ImmutableInterface`	`add_with_arguments`, `sid`, `sid_ignore`, `with_arguments`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

class pymor.algorithms.timestepping.TimeStepperInterface[source]¶

Bases: pymor.core.interfaces.ImmutableInterface

Interface for time-stepping algorithms.

Algorithms implementing this interface solve time-dependent problems of the form

M * d_t u + A(u, mu, t) = F(mu, t).

Time-steppers used by InstationaryDiscretization have to fulfill this interface.

Methods

`TimeStepperInterface`	`solve`
`ImmutableInterface`	`generate_sid`, `with_`, `__setattr__`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ImmutableInterface`	`add_with_arguments`, `sid`, `sid_ignore`, `with_arguments`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

solve(initial_time, end_time, initial_data, operator, rhs=None, mass=None, mu=None, num_values=None)[source]¶

Apply time-stepper to the equation

M * d_t u + A(u, mu, t) = F(mu, t).

Parameters

initial_time: The time at which to begin time-stepping.
end_time: The time until which to perform time-stepping.
initial_data: The solution vector at initial_time.
operator: The Operator A.
rhs: The right-hand side F (either VectorArray of length 1 or Operator with range.dim == 1). If None, zero right-hand side is assumed.
mass: The Operator M. If None, the identity operator is assumed.
mu: Parameter for which operator and rhs are evaluated. The current time is added to mu with key _t.
num_values: The number of returned vectors of the solution trajectory. If None, each intermediate vector that is calculated is returned.

Returns

VectorArray containing the solution trajectory.

pymor.algorithms.timestepping.explicit_euler(A, F, U0, t0, t1, nt, mu=None, num_values=None)[source]¶

pymor.algorithms.timestepping.implicit_euler(A, F, M, U0, t0, t1, nt, mu=None, num_values=None, solver_options='operator')[source]¶

to_matrix module¶

class pymor.algorithms.to_matrix.ToMatrixRules[source]¶

Bases: pymor.algorithms.rules.RuleTable

Methods

`RuleTable`	`append_rule`, `apply`, `apply_children`, `get_children`, `insert_rule`, `replace_children`
`BasicInterface`	`disable_logging`, `enable_logging`, `has_interface_name`, `implementor_names`, `implementors`

Attributes

`ToMatrixRules`	`action_AdjointOperator`, `action_BlockOperator`, `action_ComponentProjection`, `action_Concatenation`, `action_IdentityOperator`, `action_LincombOperator`, `action_NumpyMatrixOperator`, `action_VectorArrayOperator`, `action_ZeroOperator`, `rules`
`BasicInterface`	`logger`, `logging_disabled`, `name`, `uid`

pymor.algorithms.to_matrix.to_matrix(op, format=None, mu=None)[source]¶

Transfrom construction of NumpyMatrixOperators to NumPy or SciPy array

Parameters

op: Operator.
format: Format of the resulting SciPy spmatrix. If None, a dense format is used.
mu: Parameter.

Returns

res: Equivalent matrix.

pymor.algorithms package¶

Submodules¶

adaptivegreedy module¶

basic module¶

ei module¶

error module¶

genericsolvers module¶

gram_schmidt module¶

greedy module¶

image module¶

newton module¶

pod module¶

preassemble module¶

projection module¶

rules module¶

timestepping module¶

to_matrix module¶

Table Of Contents

Previous topic

Next topic

This Page

reduced_discretization:	The reduced `Discretization` obtained for the computed basis.
extensions:	Number of greedy iterations.
max_errs:	Sequence of maximum errors during the greedy run.
max_err_mus:	The parameters corresponding to `max_errs`.
max_val_errs:	Sequence of maximum errors on the validation set.
max_val_err_mus:	The parameters corresponding to `max_val_errs`.
refinements:	Number of refinements made in each extension step.
training_set_sizes:	The final size of the training set in each extension step.
time:	Duration of the algorithm.
reduction_data:	Reduction data returned by the last reductor call.

errors:	Sequence of maximum approximation errors during greedy search.
triangularity_errors:	Sequence of maximum absolute values of interoplation matrix coefficients in the upper triangle (should be near zero).

dofs:	`NumPy array` of the DOFs at which the `Operators` have to be evaluated.
basis:	`VectorArray` containing the generated collateral basis.
errors:	Sequence of maximum approximation errors during greedy search.
triangularity_errors:	Sequence of maximum absolute values of interoplation matrix coefficients in the upper triangle (should be near zero).

mus:	The test `Parameters` which have been considered.
basis_sizes:	The reduced basis dimensions which have been considered.
norms:	`NumPy array` of the norms of the high-dimensional solutions w.r.t. all given test `Parameters`, reduced basis dimensions and norms in `error_norms`. (Only present when `error_norms` has been specified.)
max_norms:	Maxima of `norms` over the given test `Parameters`.
max_norm_mus:	`Parameters` corresponding to `max_norms`.
errors:	`NumPy array` of the norms of the model reduction errors w.r.t. all given test `Parameters`, reduced basis dimensions and norms in `error_norms`. (Only present when `error_norms` has been specified.)
max_errors:	Maxima of `errors` over the given test `Parameters`.
max_error_mus:	`Parameters` corresponding to `max_errors`.
rel_errors:	`errors` divided by `norms`. (Only present when `error_norms` has been specified.)
max_rel_errors:	Maxima of `rel_errors` over the given test `Parameters`.
max_rel_error_mus:	`Parameters` corresponding to `max_rel_errors`.
error_norm_names:	Names of the given `error_norms`. (Only present when `error_norms` has been specified.)
estimates:	`NumPy array` of the model reduction error estimates w.r.t. all given test `Parameters` and reduced basis dimensions. (Only present when `estimator` is `True`.)
max_estimate:	Maxima of `estimates` over the given test `Parameters`.
max_estimate_mus:	`Parameters` corresponding to `max_estimates`.
effectivities:	`errors` divided by `estimates`. (Only present when `estimator` is `True` and `error_norms` has been specified.)
min_effectivities:	Minima of `effectivities` over the given test `Parameters`.
min_effectivity_mus:	`Parameters` corresponding to `min_effectivities`.
max_effectivities:	Maxima of `effectivities` over the given test `Parameters`.
max_effectivity_mus:	`Parameters` corresponding to `max_effectivities`.
errors:	`NumPy array` of the reduced system matrix conditions w.r.t. all given test `Parameters` and reduced basis dimensions. (Only present when `conditions` is `True`.)
max_conditions:	Maxima of `conditions` over the given test `Parameters`.
max_condition_mus:	`Parameters` corresponding to `max_conditions`.
custom_values:	`NumPy array` of custom function evaluations w.r.t. all given test `Parameters`, reduced basis dimensions and functions in `custom`. (Only present when `custom` has been specified.)
max_custom_values:	Maxima of `custom_values` over the given test `Parameters`.
max_custom_values_mus:	`Parameters` corresponding to `max_custom_values`.
time:	Time (in seconds) needed for the error analysis.
summary:	String containing a summary of all computed quantities for the largest (last) considered basis size.
figure:	The figure containing the generated plots. (Only present when `plot` is `True`.)

error_sequence:	`NumPy array` containing the residual norms after each iteration.
stages:	See `return_stages`.
residuals:	See `return_residuals`.