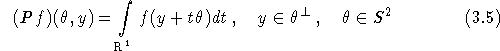
This formula inverts the ray transform
which comes up e.g. in 3D emission tomography (PET, Defrise et al. (1989)). If 
is restricted to a plane, then we have simply the Radon transform in this plane, and we can
reconstruct f in that plane by any of the methods in the previous section. In practice
g = Pf is measured for 
where 
. In Orlov's formula
(Orlov (1976)), 
is a spherical zone around the equator, i.e.
where 
, 
are the spherical coordinates of 
and 
. Then,
where 
is the Laplacian acting on x and 
is the length of the intersection of with the plane spanned by 
. The first
formula of (3.6) is - up to - a backprojection, while the second one a
convolution in 
. Thus an implementation of (3.6) is again a filtered backprojection algorithm.
P can also be inverted by the Fourier transform. We have
where `` 
'' denotes the (n-1)-dimensional Fourier transform in on the left hand side and the Fourier transform in 
on the right hand side.
Assume that satisfies the Orlov condition: Every equatorial circle of 
meets . Note that the set - the spherical zone - we used above in Orlov's formula satisfies this condition. From (3.7) it follows that f is uniquely determined by 
for under the Orlov condition. Namely if 
is arbitrary, then Orlov's condition says that there exists 
, and 
is determined from (3.7).
