In 3D CT one reconstructes a from the values of
where v runs through the source curve V outside supp(a) and 
. Most reconstruction formulas make use of an intermediate function
where h is homogeneous of degree -2 and a function F on 
derived from G by
The reconstruction formula then reads
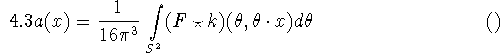
where the convolution with the 1D function k in the second argument. It can be shown that (4.1-3) is in fact a reconstruction formula provided that
For the proof we start out from
with the 3D Radon transform [49], hence 
. Then, (4.3) is compared with (2.4) for n = 3, i.e.
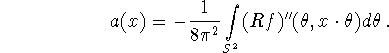
This coincides with (4.3) if (4.4) holds.
The simplest choice for h, k is 
, 
. In this case, both 
, 
are local. We obtain Grangeat's inversion formula [19]
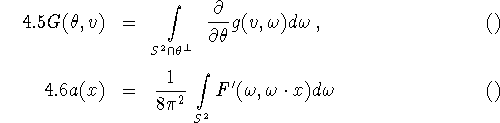
where 
is the derivative in direction 
with respect to the second argument and 
is the partial derivative with respect to the second argument. In order to apply (4.5-6), 
is needed for each plane 
meeting supp(a). Since F is obtained from G by means of (4.2) we need for each such plane
a source v in that plane. In view of (4.5) this means that g is available for a neighbourhood of the fan in that plane converging to the source v. This is Grangeat's completeness condition.
The inversion formulas of Tuy [53], B. Smith [50] and Gelfand and Goncharov
[17] can be obtained by putting 
, 
and 
, 
, respectively [12]. These formulas are not as useful as Grangeat's formula since h is no longer local.
In practice 
is measured on a detector plane 
where 
is the orthogonal projection of v onto 
. Putting 
, (4.1) assumes the form
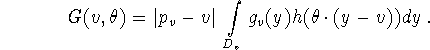
Introducing an orthogonal system 
in 
we obtain in the Grangeat case (4.5)
where 
, R is the 2D Radon transform and 
the gradient of 
. Thus Grangeat's formula can be implemented by computing line integrals in the detector plane, followed by a 3D backprojection (4.6). An implementation analogous to the filtered backprojection algorithm of 2D tomography can be found in [12].
In 3D emission CT, the requirements are quite different. In PET one puts the object into a vertical cylinder whose interior surface is covered by detectors. With such an arrangement one measures the X-ray transform for all lines joining two points on the mantle of the cylinder. In principle one could do the reconstruction layer by layer, using only horizontal lines in each layer. However, all the information contained in the oblique rays would be lost.
A formula which at least partially copes with this situation is
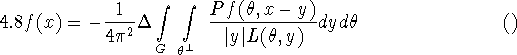
where 
is a spherical zone around the equator and 
is the length of the intersection of G and the plane spanned by , y [41]. With (4.8) one still has problems near the openings of the cylinder. More satisfactory reconstruction formulas based on the principle of the stationary phase have been given in [11].