In the description of the mathematical models we restrict ourselves to those features which are important for the mathematical scientist. For physical and medical aspects see [35], [6], [32].
(a) Transmission CT.
This is the original and simplest case of CT. In transmission tomography one probes an object with non diffracting radiation, e.g. x-rays for the human body. If ![]() is the intensity of the source, a(x) the linear attenuation coefficient of the object at point x, L the ray along which the radiation propagates, and I the intensity past the object, then
is the intensity of the source, a(x) the linear attenuation coefficient of the object at point x, L the ray along which the radiation propagates, and I the intensity past the object, then
![]()
In the simplest case the ray L may be thought of as a straight line. Modeling L as strip or cone, possibility with a weight factor to account for detector inhomogeneites may be more appropriate. In (2.1) we neglegt the dependence of a from the energy (beam hardening effect) and other non linear phenomena (e.g. partial volume effect).
The mathematical problem in transmission tomography is to determine a from measurements of I for a large set of rays L. If L is simply the straight line connecting the source ![]() with the detector
with the detector ![]() , (2.1) gives rise to the integrals
, (2.1) gives rise to the integrals
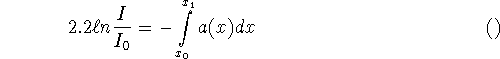
where dx is the restriction to L of the Lebesgue measure in ![]() . We have to compute a in a domain
. We have to compute a in a domain ![]() from the values of (2.2) where
from the values of (2.2) where ![]() ,
, ![]() run through certain subsets of
run through certain subsets of ![]() .
.
For n = 2, (2.2) is simply a reparametrization of the Radon transform
![]()
where ![]() . Thus our problem is in principle solved by Radon's inversion formula
. Thus our problem is in principle solved by Radon's inversion formula
![]()
where
![]()
is the so-called backprojection and
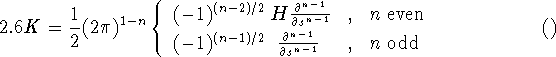
with H the Hilbert transform [39]. In fact the numerical implementation of (2.4) leads to the filtered backprojection algorithm which is the standard algorithm in commercial CT scanners, see section 3.
For n = 3, the relevant integral transform is the x-ray transform
![]()
where ![]() and
and ![]() .
. ![]() admits a similar inversion formula as R, to wit
admits a similar inversion formula as R, to wit
![]()
with K very similar to (2.6) and
![]()
where ![]() is the orthogonal projection onto
is the orthogonal projection onto ![]() . Unfortunately, (2.7) is not as useful as (2.4). The reason is that (2.7) requires g for all
. Unfortunately, (2.7) is not as useful as (2.4). The reason is that (2.7) requires g for all ![]() and
and ![]() , i.e. (2.2) has to be available for all
, i.e. (2.2) has to be available for all ![]() ,
, ![]() . This is not practical. Also, it is not necessary for unique reconstruction of a. In fact it can be shown that a can be recovered uniquely from (2.2) with sources
. This is not practical. Also, it is not necessary for unique reconstruction of a. In fact it can be shown that a can be recovered uniquely from (2.2) with sources ![]() on a circle surrounding supp(a) and
on a circle surrounding supp(a) and ![]() . Unfortunately the determination of a in such an arrangement is, though uniquely possible, highly unstable. The condition of stability is the following: Each plane meeting supp(a) must contain at least one source [16]. This condition is obviously violated for sources on a circle. Cases in which the condition is satisfied include the helix and a pair of orthogonal circles. A variety of inversion formulae has been derived, see section 4.
. Unfortunately the determination of a in such an arrangement is, though uniquely possible, highly unstable. The condition of stability is the following: Each plane meeting supp(a) must contain at least one source [16]. This condition is obviously violated for sources on a circle. Cases in which the condition is satisfied include the helix and a pair of orthogonal circles. A variety of inversion formulae has been derived, see section 4.
If scatter is to be included, a transport model is more appropriate. Let ![]() be the density of the particles at x travelling (with speed 1) in direction
be the density of the particles at x travelling (with speed 1) in direction ![]() . Then,
. Then,
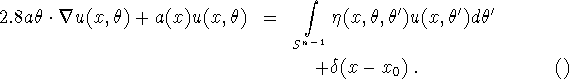
Here, ![]() is the probability that a particle at x travelling in direction
is the probability that a particle at x travelling in direction ![]() is scattered in direction
is scattered in direction ![]() . Again we neglect dependence on energy.
. Again we neglect dependence on energy. ![]() is the Dirac
is the Dirac ![]() -function modeling a source of unit strength. (2.2a) holds in a domain
-function modeling a source of unit strength. (2.2a) holds in a domain ![]() of
of ![]() , and
, and ![]() . Since no radiation comes in from outside we have
. Since no radiation comes in from outside we have
![]()
where ![]() is the exterior normal on
is the exterior normal on ![]() at
at ![]() . (4.1) is now replaced by
. (4.1) is now replaced by
![]()
The problem of recovering a from (2.8) in much harder. An explicit formula for a such as (2.4) has not become known and is unlikely to exist. Nevertheless numerical methods have been developed for special choices of ![]() [3], [7]. The situation gets even more difficult if one takes into account that, strictly speaking,
[3], [7]. The situation gets even more difficult if one takes into account that, strictly speaking, ![]() is object dependent and hence not known in advance. (2.8) is a typical example of an inverse problem for a partial differential equation. In an inverse problem one has to determine the differential equation - in our case a,
is object dependent and hence not known in advance. (2.8) is a typical example of an inverse problem for a partial differential equation. In an inverse problem one has to determine the differential equation - in our case a, ![]() - from information about the solution - in our case (2.8c).
- from information about the solution - in our case (2.8c).
(b) Emission CT.
In emission tomography one determines the distribution f of radiating sources in the interior of an object by measuring the radiation outside the object in a tomographic fashion. Let again ![]() be the density of particles at x travelling in direction
be the density of particles at x travelling in direction ![]() with speed 1, and let a be the attenuation distribution of the object. (This is the quantity which is sought for in transmission CT). Then,
with speed 1, and let a be the attenuation distribution of the object. (This is the quantity which is sought for in transmission CT). Then,
![]()
This equation holds in the object region ![]() for each
for each ![]() . Again there exists no incoming radiation, i.e.
. Again there exists no incoming radiation, i.e.
![]()
while the outgoing radiation
![]()
is measured and hence known. (2.9) again constitutes an inverse problem for a transport equation. For a known, (2.9a-b) is readily solved to yield
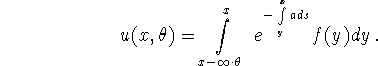
Thus (2.9c) leads to the integral equation
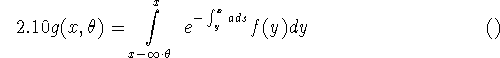
for f. Apart from the exponential factor, (2.10) is identical - up to notation - to the integral equation in transmission CT. Except for very special cases - e.g. a constant in a known domain [52], [42] no explicit inversion formulas are available. Numerical techniques have been developed but are considered to be slow. Again the situation becomes worse if scatter is taken into account. This can be done by simply adding the scattering integral in (2.8a) to the right hand side of (2.9a).
What we have described to far is called SPECT (= single particle emission CT). In PET (= positron emission tomography) the sources eject the particles pairwise in opposite directions. They are detected in coincidence mode, i.e. only events with two particles arriving at opposite detectors at the same time are counted. (1.10) has to be replaced by
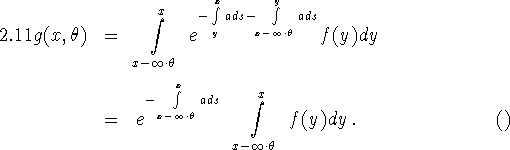
Thus PET is even closer to the case of transmission CT. If a is known, we simply have to invert the x-ray transform. Inversion formulas which can make use of the data collected in PET are available, see section 3.
The main problems in emission CT are unknown attenuation, noise, and scatter. For the attenuation problem, the ideal mathematical solution would be a method for determining f and a in (2.9) simultaneously. Under strong assumption on a (e.g. a constant in a known region [26], a affine distortion of a prototype [37], a close to a known distribution [8]) encouraging results have been obtained. Theoretical results based on the transport formulation have been obtained, even for models including scatter [43]. But a clinically useful way of determining a from the emission data has not yet been found.
Noise and scatter are stochastic phenomena. Thus, besides models using integral equations, stochastic models have been set up for emission tomography [48]. These models are completely discrete. We subdivide the reconstruction region into m pixels or voxels. The number of events in pixel/voxel j is a Poisson random variable ![]() whose mathematical expection
whose mathematical expection ![]() is a measure for the activity in pixel/voxel j. The vector
is a measure for the activity in pixel/voxel j. The vector ![]() is the sought - for quantity. The vector
is the sought - for quantity. The vector ![]() of measurements is considered as realization of the random variable
of measurements is considered as realization of the random variable ![]() where
where ![]() is the number of events detected in detector i. The model is determined by the (n,m)-matrix
is the number of events detected in detector i. The model is determined by the (n,m)-matrix ![]() whose elements are
whose elements are
![]() (event in pixel/voxel j detected in detector i)
(event in pixel/voxel j detected in detector i)
where P denotes probability. We have ![]() .
. ![]() is determined from g by the maximum liklihood method. A numerical method for doing this is the EM (= expection maximation) algorithm. In its basic form it reads
is determined from g by the maximum liklihood method. A numerical method for doing this is the EM (= expection maximation) algorithm. In its basic form it reads
![]()
where division and multiplication are to be understood component wise. The problem with the EM-algorithm is that it is only semi-convergent, i.e. noise is amplified at high iteration numbers. This is known as the checkerboard effect.
Various suggestions have been made to get rid of this effect. The most exciting and interesting ones use ``prior information'' and attempt to maximize ``posterior likelihood''. Thus f is assumed to have a prior probability distribution, called a Gibbs-Markov random field ![]() , which gives preference to certain functions f [46], [21], [18]. Most prior
, which gives preference to certain functions f [46], [21], [18]. Most prior ![]() simply add a penalty term to the likelihood function to account for correction between neighboring pixels and do not use biological information. However if
simply add a penalty term to the likelihood function to account for correction between neighboring pixels and do not use biological information. However if ![]() is carefully chosen so that piecewise constant functions f with smooth boundaries forming the region of constancy are preferred then the noise amplification at high iteration numbers can be avoided. The question remains as to whether this conclusion will remain valid for function f which are assigned low probability by
is carefully chosen so that piecewise constant functions f with smooth boundaries forming the region of constancy are preferred then the noise amplification at high iteration numbers can be avoided. The question remains as to whether this conclusion will remain valid for function f which are assigned low probability by ![]() - or, more to the point - whether ``real'' emission densities f will be well-resolved by this Bayesian method. An ROC study (e.g. double-blind trials where radiologists are to find lesions from images produced by two different algorithms) concluded that maximum likelihood methods were superior to the filtered backprojection algorithm (see section 3) in certain clinical applications. The same type of study is needed to determine whether or not Gibbs priors will improve the maximum likelihoof reconstruction (stopped short of convergence to avoid noise amplification) on real data.
- or, more to the point - whether ``real'' emission densities f will be well-resolved by this Bayesian method. An ROC study (e.g. double-blind trials where radiologists are to find lesions from images produced by two different algorithms) concluded that maximum likelihood methods were superior to the filtered backprojection algorithm (see section 3) in certain clinical applications. The same type of study is needed to determine whether or not Gibbs priors will improve the maximum likelihoof reconstruction (stopped short of convergence to avoid noise amplification) on real data.
(c) Ultrasound CT
X-rays travel along straight lines. For other sources of radiation, such as ultrasound and microwaves, this is no longer the case. The paths are no longer straight, and their exact shape depends on the internal structure of the object. We can no longer think in terms of simple projections and linear integral equations. More sophisticated non linear models have to be used.
In the following we consider an object ![]() with refractive index n. We assume n = 1 outside the object.
The object is probed by a plane wave
with refractive index n. We assume n = 1 outside the object.
The object is probed by a plane wave
![]()
with wave number ![]() ,
, ![]() the wave length, travelling in the direction
the wave length, travelling in the direction ![]() . The resulting wave
. The resulting wave ![]() satisfies the reduced wave equation
satisfies the reduced wave equation
![]()
plus suitable boundary conditions at infinity. The inverse problem to be solved is now the following. Assume that
![]()
is known outside ![]() . Determine f inside
. Determine f inside ![]() !
!
Uniqueness and stability of the inverse problem (2.12) has recently been settled [36]. However, stability is only logarithmic [2], i.e. a data error of size ![]() results in a reconstruction error
results in a reconstruction error ![]() . Numerical algorithms did not emerge from this work.
. Numerical algorithms did not emerge from this work.
Numerical methods for (2.12) are mostly based on linearizations, such as the Born and Rytov approximation [13]. In order to derive the Born approximation, one rewrites (2.12a) as
![]()
where G is an appropriate Green's function. For n = 3, we have
![]()
The Born approximation is now obtained by assuming ![]() in the integral in (2.13). With this approximation, (2.12b) reads
in the integral in (2.13). With this approximation, (2.12b) reads
![]()
This is a linear integral equation for f, valid for all x outside the object and for all measured directions ![]() .
.
Numerical methods based on (2.15) - and a similar equation for the Rytov approximation - have become known as diffraction tomography. Unfortunately, the assumptions underlying the Born- and Rytov approximations are not satisfied in medical imaging. Thus, the reconstructions of f obtained from (2.15) are very poor. However, we may use (2.15) to get some encouraging information about stability. For |x| large, (2.15) assumes the form
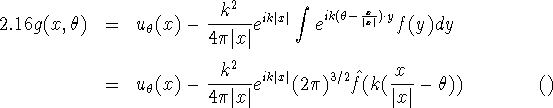
with ![]() the Fourier transform of f. (2.16) determines
the Fourier transform of f. (2.16) determines ![]() within a ball of radius
within a ball of radius ![]() from the data (2.12b) in a completely stable way. We conclude that the stability of the inverse problem (2.12) is much better than logarithmic. If the resolution is restricted to spatial frequencies below
from the data (2.12b) in a completely stable way. We conclude that the stability of the inverse problem (2.12) is much better than logarithmic. If the resolution is restricted to spatial frequencies below ![]() - which is perfectly reasonable from a physical point of view - then we can expect (2.12) to be perfectly stable.
- which is perfectly reasonable from a physical point of view - then we can expect (2.12) to be perfectly stable.
So far we considered plane wave irradiation at fixed frequency, and we worked in the frequency domain. Time domain methods are conceivable as well. We start out from the wave equation
![]()
with the propagation speed c assumed to be 1 outside the object. With ![]() a source outside the object we consider the initial conditions
a source outside the object we consider the initial conditions
![]()
We want to determine c inside the object from knowing
![]()
for many sources ![]() and receivers
and receivers ![]() outside the object. In the one dimensional case, the inverse problem (2.17) can be solved by the famous Gelfand-Levitan method in a stable way. It is not clear how Gelfand-Levitan can be extended to dimensions two and three. The standard methods use sources and receivers on all of the boundary of the object. This is not practical in medical imaging. However, for reduced data sets, comparable to those in 3D X-ray tomography, we do not know how to use Gelfand-Levitan, nor do we know anything about stability.
outside the object. In the one dimensional case, the inverse problem (2.17) can be solved by the famous Gelfand-Levitan method in a stable way. It is not clear how Gelfand-Levitan can be extended to dimensions two and three. The standard methods use sources and receivers on all of the boundary of the object. This is not practical in medical imaging. However, for reduced data sets, comparable to those in 3D X-ray tomography, we do not know how to use Gelfand-Levitan, nor do we know anything about stability.
Of course one can always solve the nonlinear problem (2.17) by a Newton type method. Such methods have been developed [23], [30]. They suffer from excessive computing time and from their apparent inability to handle large wave numbers k.
(d) Optical tomography
Here one uses NIR (= near infra-red) lasers for the illumination of the body. The process is now described by the transport equation
![]()
![]()
for the density ![]() of the particles at
of the particles at ![]() flying in direction
flying in direction ![]() at time t.
at time t. ![]() and b are the sought - for tissue parameters. The scattering kernel
and b are the sought - for tissue parameters. The scattering kernel ![]() is assumed to be known. The source term f is under the control of the experimenter. Together with the initial and boundary conditions
is assumed to be known. The source term f is under the control of the experimenter. Together with the initial and boundary conditions
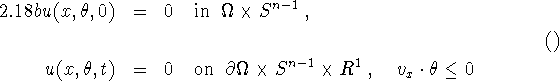
(1.18a) has a unique solution under natural conditions on a, b, ![]() and f. As in (1.1) we pose the inverse problem. Assume that we know the outward radiation
and f. As in (1.1) we pose the inverse problem. Assume that we know the outward radiation
![]()
can we determine one or both the quantities a, b?
There are essentially three methods for illuminating the object, i.e. for choosing the source term f in (2.18a). In the stationary case one puts ![]() where
where ![]() is a source point.
is a source point. ![]() is considered stationary, too. A second possibility is the light flash
is considered stationary, too. A second possibility is the light flash ![]() . Finally one can also use time harmonic illumination, in which case
. Finally one can also use time harmonic illumination, in which case ![]() . This case reduces to the stationary case with a replaced by
. This case reduces to the stationary case with a replaced by ![]() . In all three cases, the data function g of (2.18c) is measured at
. In all three cases, the data function g of (2.18c) is measured at ![]() , possibly averaged over one or both of the variables
, possibly averaged over one or both of the variables ![]() , t.
, t.
Light tomography is essentially a scattering phenomenon. This means that the scattering integral in (2.18a) is essential. It can no longer be treated merely as a perturbation as in x-ray CT. Thus the mathematical analysis and the numerical methods are expected to be quite different from what we have seen in other types of tomography.
The mathematical theory of the inverse problem (2.18) is in a deplorable state. There exist some Russian papers on uniqueness [4]. General methods have been developed, too, but apparently they have been applied to 1D problems only [44]. Nothing seems to be known about stability. The numerical methods which have become known are of the Newton type, either applied directly to the transport equation or to the so-called diffusion approximation [5], [31]. The diffusion approximation is an approximation to the transport equation by a parabolic differential equation. Since inverse problems for parabolic equations are severely ill-posed, this approach is questionable. Higher order approximations [29], [20] are hyperbolic, making the inverse problem much more stable.
As an alternative to the transport equation one can also model light tomography by a discrete stochastical model [22]. In the 2D case, break up the object into a rectangular arrangement of pixels labelled by indices i, j with ![]() and
and ![]() . Attach to each pixel the quantities
. Attach to each pixel the quantities ![]() ,
, ![]() ,
, ![]() ,
, ![]() meant to denote the probability of a forward, backward, rightward or leftward transition out of the pixel i, j with respect to the direction used to get into this pixel. For each pair of boundary pixels i, j and
meant to denote the probability of a forward, backward, rightward or leftward transition out of the pixel i, j with respect to the direction used to get into this pixel. For each pair of boundary pixels i, j and ![]() ,
, ![]() let
let ![]() be the probability that a particle that enters the object at pixel i, j will eventually leave the object at pixel
be the probability that a particle that enters the object at pixel i, j will eventually leave the object at pixel ![]() ,
, ![]() . The problem is to determine the quantities
. The problem is to determine the quantities ![]() ,
, ![]() ,
, ![]() ,
, ![]() from the values of
from the values of ![]() for all boundary pixels. Preliminary numerical tests show that this is possible, at least in principle. However, the computations are very time consuming. More seriously, they reveal a very high degree of instability.
for all boundary pixels. Preliminary numerical tests show that this is possible, at least in principle. However, the computations are very time consuming. More seriously, they reveal a very high degree of instability.
(e) Electrical Impedance Tomography
Here, the sought-for quantity is the electrical impedance ![]() of an object
of an object ![]() . Voltages are applied via electrodes on
. Voltages are applied via electrodes on ![]() , and the resulting currents at these electrodes are measured. With u the potential in
, and the resulting currents at these electrodes are measured. With u the potential in ![]() , we have
, we have
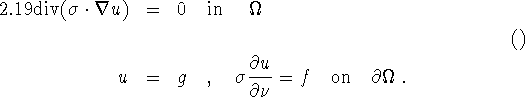
Knowing many voltage - current pairs g, f on ![]() , we have to determine
, we have to determine ![]() from (2.19).
from (2.19).
Uniqueness for the inverse problem (2.19) has recently be settled [36]. Unfortunately, the stability properties are very bad [2]. Numerical methods based on Newton's method, linearization, simple backprojection, layer stripping have been tried. All these methods suffer from the severe ill-posedness of the problem. There seems to be no way to improve stability by purely mathematical means.
(f) Magnetic Resonance Imaging (MRI)
The physical phenomena exploited here is the precession of the spin of a proton in a magnetic field of strength H about the direction of that field. The frequency of this precession is the Larmor frequency ![]() where
where ![]() is the gyromagnetic ratio. By making the magnetic field H space dependent in a controled way the local magnetization
is the gyromagnetic ratio. By making the magnetic field H space dependent in a controled way the local magnetization ![]() (together with the relaxation times
(together with the relaxation times ![]() ,
, ![]() ) can be imaged. In the following we derive the imaging equations [27].
) can be imaged. In the following we derive the imaging equations [27].
The magnetization M(x,t) caused by a magnetic field H(x,t) satisfies the Bloch equation
![]()
Here, ![]() is the i-th component of M, and
is the i-th component of M, and ![]() is the i-th unit vector i=1,2,3. The significance of
is the i-th unit vector i=1,2,3. The significance of ![]() ,
, ![]() ,
, ![]() become apparent if we solve (2.20) with the static field
become apparent if we solve (2.20) with the static field ![]() and with initial values
and with initial values ![]() . We obtain with
. We obtain with ![]()
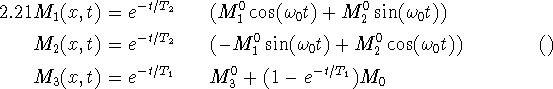
Thus the magnetization rotates in the ![]() -plane with Larmor frequency
-plane with Larmor frequency ![]() and returns to the equilibrium condition
and returns to the equilibrium condition ![]() with speed controlled by
with speed controlled by ![]() in the
in the ![]() -plane and by
-plane and by ![]() in the
in the ![]() -direction.
-direction.
In an MRI scanner one generates a field
![]()
where G and ![]() are under control. In the jargon of MRI,
are under control. In the jargon of MRI, ![]() is the static field, G the gradient, and
is the static field, G the gradient, and ![]() the radio frequency (RF) field. The input G,
the radio frequency (RF) field. The input G, ![]() produces in the detecting system of the scanner the output signal
produces in the detecting system of the scanner the output signal
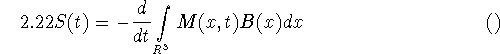
where B characterizes the detecting system. Depending on the choice of ![]() various approximation to S can be derived.
various approximation to S can be derived.
(i) ![]() is constant in the small interval
is constant in the small interval ![]() and
and ![]() (Short
(Short ![]() pulse). In that case,
pulse). In that case,
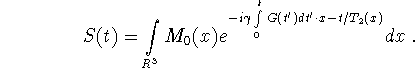
Choosing G constant for ![]() and zero otherwise we get for
and zero otherwise we get for ![]()
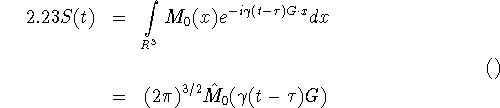
where ![]() is the 3D Fourier transform of
is the 3D Fourier transform of ![]() .
.
From here we can proceed in several ways. We can either use (2.23) to determine the 3D Fourier transform ![]() of
of ![]() and to compute
and to compute ![]() by an inverse 3D Fourier transform. This requires
by an inverse 3D Fourier transform. This requires ![]() to be known on a Cartesian grid, what can be achieved by a proper choice of the gradients or by interpolation. We can also evoke the central slice theorem to obtain the 3D Radon transform
to be known on a Cartesian grid, what can be achieved by a proper choice of the gradients or by interpolation. We can also evoke the central slice theorem to obtain the 3D Radon transform ![]() of
of ![]() by a series of 1D Fourier transforms.
by a series of 1D Fourier transforms. ![]() is recovered in turn by inverting the 3D Radon transform.
is recovered in turn by inverting the 3D Radon transform.
The main numerical problem in MRI is to reconstruct a function from inperfect measurements of its Fourier transform [34]. Not much been achied so far.
(ii) ![]() is the shaped pulse
is the shaped pulse
![]()
where ![]() is a smooth positive function supported in
is a smooth positive function supported in ![]() . Then, with
. Then, with ![]() ,
, ![]() the first to components of x, G, respectively, we have
the first to components of x, G, respectively, we have
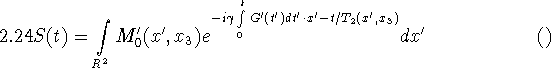
where
![]()
with a function Q essentially supported in a small neighborhood of 0. (2.24) is the 2D analogue of (2.23). So we have again the choice between Fourier imaging (i.e. computing the 2D Fourier transform from (2.24) and doing an inverse 2D Fourier transform) and projection imaging (i.e. doing a series of 1D Fourier transforms in (2.24) and inverting the 2D Radon transform).
Some of the mathematical problems of MRI, e.g. interpolation in Fourier space, are common to other techniques in medical imaging. An interesting mathematical problem occurs if the magnets to not produce suffiently homogeneous fields [33]. It calls for the reconstruction of a function from integrals over slightly curved manifolds. Even though this is a problem of classical integral geometry it has not yet found a satisfactory solution.
(g) Vector Tomography
If the domain under consideration contains a moving fluid, then the Doppler shift can be used to measure the velocity u(x) of motion. Assume the time harmonic signal ![]() is transmitted along the oriented line L. This signal is reflected by particles travelling with speed
is transmitted along the oriented line L. This signal is reflected by particles travelling with speed ![]() in the direction of L as
in the direction of L as ![]() , where
, where ![]() , c the speed of the probing signal, i.e.
, c the speed of the probing signal, i.e. ![]() is the Doppler shift. Let
is the Doppler shift. Let ![]() be the Lebesgue measure of these particles on L which move with speed
be the Lebesgue measure of these particles on L which move with speed ![]() , i.e.
, i.e. ![]() ,
, ![]() the tangent vector on L. Then the total response is
the tangent vector on L. Then the total response is
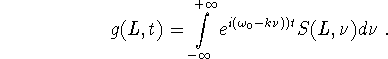
Thus S can be recovered from g by a Fourier transform. The problem is to recover u from S.
Not much is known about uniqueness. However, the first moment of S,
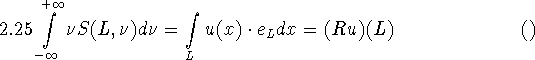
is similar to the Radon transform. One can show that curl u can be computed from Ru, and an inversion formula similar to the Radon inversion formula exists. Numerical simulations are given in [51].
(h) Tensor Tomography
As an immediate extension of transmission CT to non-isotropic media we consider a matrix valued attenuation ![]() , i,
, i, ![]() . We solve the vector differential equation
. We solve the vector differential equation
![]()
for the vector valued function ![]() . Let a be defined in a convex domain
. Let a be defined in a convex domain ![]() , and let
, and let ![]() ,
, ![]() . Then,
. Then, ![]() with a nonlinear map
with a nonlinear map ![]() depending on a. The problem is to recover a in
depending on a. The problem is to recover a in ![]() from the knowledge of
from the knowledge of ![]() for
for ![]() ,
, ![]() . For n = 1 we regain (2.1). Applications of (2.25) for n > 1 have become known in photoelasticity [1], but applications to medicine are not totally out of question.
. For n = 1 we regain (2.1). Applications of (2.25) for n > 1 have become known in photoelasticity [1], but applications to medicine are not totally out of question.
In a further extension we let a depend on the direction ![]() .
Such problems occur in the polarization of harmonic electromagnetic and elastic waves in anisotropic media. In linearized form these problems give rise to the transverse x-ray transform
.
Such problems occur in the polarization of harmonic electromagnetic and elastic waves in anisotropic media. In linearized form these problems give rise to the transverse x-ray transform
![]()
and to the longitudenal x-ray transform
![]()
(2.27) can easily be reduced to the (n-1)-dimensional x-ray transform in the plane ![]() . We only have to introduce the function
. We only have to introduce the function ![]() . Then, (2.27) provides for
. Then, (2.27) provides for ![]() all the line integrals of
all the line integrals of ![]() on
on ![]() . For (2.28), the situation is not so easy. We decompose a in its solenoidal and potential part, i.e.
. For (2.28), the situation is not so easy. We decompose a in its solenoidal and potential part, i.e.
![]()
It can be shown that ![]() can be recovered uniquely from (2.28), but
can be recovered uniquely from (2.28), but ![]() is completely undetermined [47]. This is reminiscent of vector tomography.
is completely undetermined [47]. This is reminiscent of vector tomography.