This is an extension of the Kaczmarz (1937) method for solving linear systems. It has been introduced in imaging by Gordon et al. (1970). We describe it in a more general context. We consider the linear system
where 
are bounded linear operators from the Hilbert space H into the Hilbertspace 
. With 
a positive definite operator we define an iteration step 
as follows:
If 
(provided 
is onto) and 
, then 
is the orthogonal projection of 
onto the affine subspace 
. For dim 
this is the original Kaczmarz method. Other special cases are the Landweber method
(p = 1, 
and fixed-block ART (dim 
finite, 
diagonal, see Censor and
Zenios (1997)). It is clear that there are many ways to apply (4.3) to (4.1), and we will make use of this freedom to our advantage.
One can show (Censor et al. (1983), Natterer (1986)) that (4.3) converges provided that
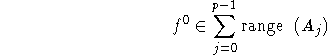
and 
. This is reminiscent of the SOR-theory of numerical analysis.
In fact we have 
where 
is the k-th SOR iterative for the linear
system 
with
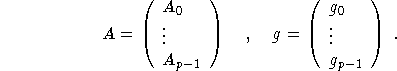
If (4.2) is consistent, ART converges to the solution of (4.2) with minimal norm in H.
Plain convergence is useful, but we can say much more about the qualitative behaviour and the speed of convergence by exploiting the special structure of the image reconstruction problems at hand. With R the Radon transform in 
we can put
where w is the weight function 
and 
. One can
show that the subspaces
the Gegenbauer polynomials of degree m (Abramowitz and Stegun (1970))
are invariant subspaces of the iteration (4.3). This has been discovered by
Hamaker and Solmon (1978). Thus it suffices to study the convergence on each subspace 
separately. The speed of convergence depends drastically on 
and
- surprisingly - on the way the directions 
are ordered. We summerize the findings of Hamaker and Solmon (1978), Natterer (1986) for the 2D case where 
.
1. Let the 
be ordered consecutively, i.e. 
, 
. For large (e.g. ) convergence on is fast for m < p large and slow for m small. This means that the high frequency parts of f (such as noise) are recovered first, while the overall features of f become visible only in the later iterations. For small (e.g. 
) the opposite is the case.
This explains why the first ART iterates for look terrible and why surprisingly small relaxation factors (e.g. ) are used in tomography.
2. Let be distributed at random in 
and . Then the convergence is fast on all , m < p. The same is true for more
sophisticated arrangements of the , such as for p = 18 (Hamaker and Solmon
(1978))
or similarly for p = 30 in Herman and Meyer (1993).
The practical consequence is that a judicious choice of directions may well speed up the convergence tremendously. Often it suffices to do only 1-3 steps if the right ordering is chosen. This has been observed also for the EM iteration (see below).
Note that the with 
are irrelevant since they describe those details in f which cannot be recovered from p projections because they are below the resolution limit.
This is a result of the resolution analysis in Natterer (1986).
