Assume again that g = Pf is known for ![]() .
.
We want to derive an inversion procedure similar to the one in section 2.1. With the backprojection
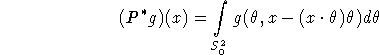
we have again
![]()
provided that ![]() . Again the convolutions on the left hand right hand side have
different meanings. Explicitly this reads
. Again the convolutions on the left hand right hand side have
different meanings. Explicitly this reads
which corresponds to (2.2). As in (2.2) we express the relationship
![]() in Fourier space, obtaining
in Fourier space, obtaining
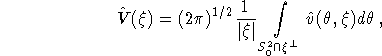
see Colsher (1980). In order to get an inversion formula for P we have to determine v such that ![]() or
or ![]() , i.e.
, i.e.
A solution ![]() independent of
independent of ![]() is
is
![]()
where ![]() is the length of
is the length of ![]() . For the spherical zone
. For the spherical zone ![]() from section 3.4 with
from section 3.4 with ![]() ,
, ![]() ,
, ![]() a constant with
a constant with ![]() , Colsher computed
, Colsher computed ![]() explicitly. With
explicitly. With ![]() be obtained
be obtained
Filters such as the Colsher filter (3.10) do not have small support. This means that g in (3.8) has to be known in all of ![]() . Often g is only available
in part of
. Often g is only available
in part of ![]() (truncated projections). Let us choose
(truncated projections). Let us choose
where ![]() from section (3.4) and
from section (3.4) and ![]() is a horizontal unit vector. Since (3.11) is constant in the vertical direction, v is a
is a horizontal unit vector. Since (3.11) is constant in the vertical direction, v is a ![]() -function in the vertical variable. Hence the
integral on the right hand side of (3.8) reduces to an integral over horizontal lines in
-function in the vertical variable. Hence the
integral on the right hand side of (3.8) reduces to an integral over horizontal lines in ![]() , making it possible to handle truncated projections. Unfortunately,
(3.11) does not quite satisfy
, making it possible to handle truncated projections. Unfortunately,
(3.11) does not quite satisfy ![]() , i.e. it does not provide an exact inversion. Instead we only have
, i.e. it does not provide an exact inversion. Instead we only have
![]()
where ![]() ,
, ![]() .
This is close to
.
This is close to ![]() if
if ![]() is small. In this case reconstruction from truncated projections is possible, at least approximately.
is small. In this case reconstruction from truncated projections is possible, at least approximately.