Seminarvortrag: Das freie skalare Feld
von Andreas Wielenberg
am 22.04 1998
Seminar über Teilchen- und Kernphysik, SS 1998
G. Münster, M. Stingl, A. Weiguny
- Das Gaußsche Integral
Wir hatten bei der Berechnung des Propagators für das freie Teilchen schon das Gaußsche Integral
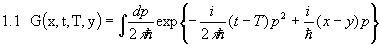
für einen Freiheitsgrad kennengelernt. Dieses Integral ist vom allgemeinen Typ
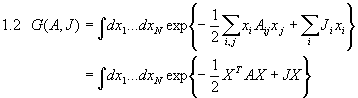
für reelle xi und N Freiheitsgrade mit einer positiv definiten symmetrischen Matrix A und einer Quelle J. Uns stellt sich zunächst die Aufgabe dieses Integral zu berechnen. Dazu werden wir versuchen, das bekannte Gaußsche Integral
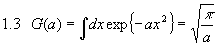
zu verwenden. Offenbar können wir 1.2 mit Hilfe von 1.3 dann ausführen, wenn es uns gelingt, die Matrix A zu diagonalisieren. Wie aus der Algebra bekannt, ist A durch eine Rotation diagonalisierbar und außerdem invertierbar. Wir führen zunächst die Variablentransformation
Y=X-A-1J, um die Terme in X und J zu trennen. Da wir es mit einer Verschiebung zu tun haben, bleibt das Maß erhalten:  .
.
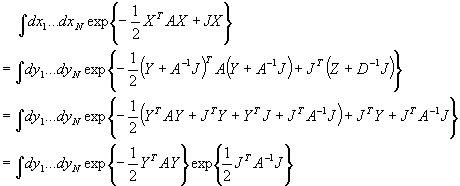
Jetzt wenden wir die Rotation
R an, die A diagonalisiert:
D=RART, wobei 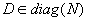 und mit RY=Z und daher
und mit RY=Z und daher  erhalten wir:
erhalten wir:
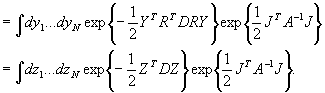
Da D eine Diagonalmatrix ist, folgt:
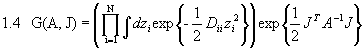 .
.
Mit 1.3 und wegen 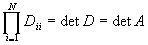 erhalten wir als Endergebnis:
erhalten wir als Endergebnis:
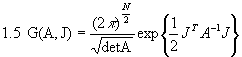 .
.
Ebenso beweist man für Paare konjugiert komplexer Variablen und hermitesche Matrizen H:
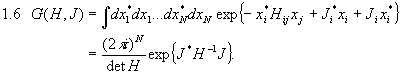
Wir können nun noch den Übergang von endlich vielen Freiheitsgraden zu unendlich vielen machen, indem wir die Variable xi durch das Feld 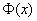 (
(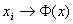 ) ersetzen. Um ein konvergentes Ergebnis zu erhalten, müssen wir das richtige Maß benützen und den vorher unterdrückten Faktor
) ersetzen. Um ein konvergentes Ergebnis zu erhalten, müssen wir das richtige Maß benützen und den vorher unterdrückten Faktor 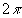 wieder in das Integral schreiben. Wir erhalten dann die Formeln:
wieder in das Integral schreiben. Wir erhalten dann die Formeln:
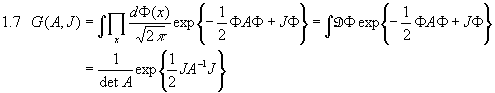
und
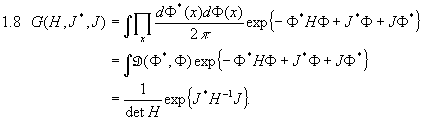
Beide Formeln werden uns beim Lösen von Pfadintegralen helfen.
- Funktionalableitungen
Für die weitere Formulierung der Feldtheorie wird sich die Funktionalableitung als wichtiges Hilfsmittel erweisen. Die Funktionalableitung ist die Übertragung der bekannten Ableitung in den Funktionenraum und wird wie folgt definiert.
Sei
F ein Funktional auf dem Funktionenraum C,, 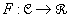 . Dann definiert man die Funktionalableitung
. Dann definiert man die Funktionalableitung  für
für  durch:
durch:
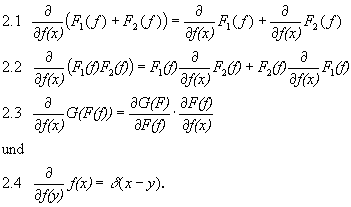
Man kann sich dann noch vor Augen führen, daß diese Ableitungsvorschrift sich auch aus

für alle (beschränkten) Funktionen 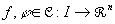 gewinnen ließe.
gewinnen ließe.
- Das Wicksche Theorem
Wir werden uns nun für Gaußsche Integrale der Form
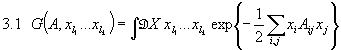
interessieren.
Die oben entwickelte Technik der Funktionalableitungen erlaubt uns dieses Integral folgendermaßen zu schreiben, wobei wir den kontinuierlichen Fall immer implizit mit betrachten:
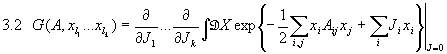
mit 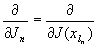 im kontinuierlichen Fall. Mit 1.5 erhalten wir als Endergebnis
im kontinuierlichen Fall. Mit 1.5 erhalten wir als Endergebnis
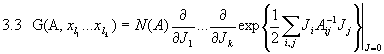
Um die Korrelationsfunktionen zu finden, betrachtet man:
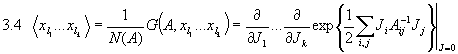 .
.
Damit erhält man zum Beispiel für k=1:
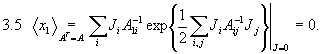
Man beachte, daß die ® aus dem Exponenten durch die Differentiation verschwinden. Für k=2 erhält man:
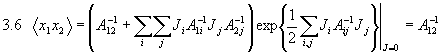 .
.
Im kontinuierlichen Grenzfall bedeutet 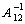 natürlich
natürlich 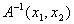 . Für k=3:
. Für k=3:
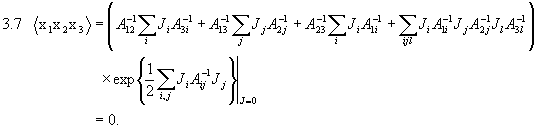
Damit wird dann für k=4 das folgende Ergebnis plausibel:
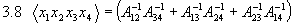 .
.
Induktiv erhalten wir so das Wicksche Theorem für Gaußintegrale:
 .
.
Dieses Theorem gibt es auch im Zusammenhang mit Operatoren. Wir verweisen auf den Anhang.
- Die Klein û Gordon û Gleichung
Da die klassische Quantenmechnik nicht kovariant formuliert ist, stellt sich uns zunächst die Aufgabe, das kovariante Äquivalent der freien Schrödingergleichung zu finden. Mit dem Viererimpuls
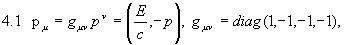
folgt wegen
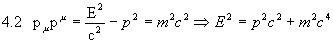
über das Korrespondenzprinzip
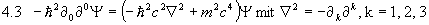 .
.
Geht man nun noch zu natürlichen Einheiten 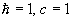 über, so erhält man die übliche Form der Klein û Gordon û Gleichung:
über, so erhält man die übliche Form der Klein û Gordon û Gleichung:
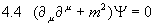 .
.
Diese beschreibt die freie Bewegung spinloser Teilchen (Mesonen) der Masse mý. Hierbei ist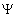 eine skalare Funktion und man unterscheidet zwei Fälle: Ist
eine skalare Funktion und man unterscheidet zwei Fälle: Ist 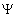 reell, so trägt das Teilchen keine Ladung , für komplexe
reell, so trägt das Teilchen keine Ladung , für komplexe 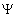 ist eine Ladung dagegen erlaubt. Wir behandeln im weiteren nur das reelle skalare Feld.
ist eine Ladung dagegen erlaubt. Wir behandeln im weiteren nur das reelle skalare Feld.
- Relativistische Formulierung der Feldtheorie
Analog zur klassischen (Punkt-) Mechanik wird die Lagrange-Funktion auch für ein Feld 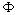 definiert. Darüber gelangt man zur LagrangeûDichte
definiert. Darüber gelangt man zur LagrangeûDichte
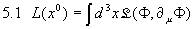 .
.
Damit kann man das Wirkungsintergral besonders einfach definieren:
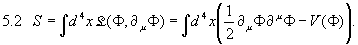
Aus dem Variationsprinzip 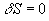 mit den Nebenbedingungen
mit den Nebenbedingungen 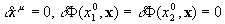 erhält man wiederum die Euler-Lagrange-Gleichungen für
erhält man wiederum die Euler-Lagrange-Gleichungen für 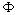 :
:
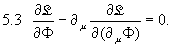
Das zu 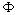 konjugierte Impuls-Feld lautet dann
konjugierte Impuls-Feld lautet dann
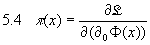
und man erhält die Hamiltondichte
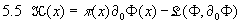 .
.
Das freie skalare Feld hat die Lagrange-Dichte
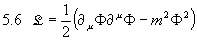
Und somit gilt
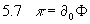
und
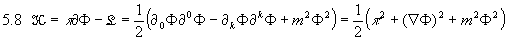
Wegen  folgt mit den Euler û Lagrange - Gleichungen für das freie skalare Feld aus 5.6:
folgt mit den Euler û Lagrange - Gleichungen für das freie skalare Feld aus 5.6:
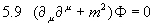 .
.
Dies hätten wir aus 5.6 auch anders erhalten können: partielle Integration liefert:
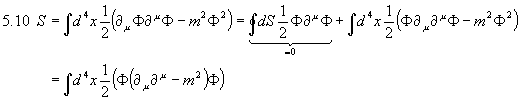
Aus der Stationarität der Wirkung folgt wiederum 5.9. Das Oberflächenintegral verschwindet, wenn wir die physikalische Randbedingung an die Felder stellen, daß sie und ihre Ableitungen im Unendlichen hinreichen rasch verschwinden.
Wir können damit das freie skalare Feld und die Lösung der Klein-Gordon-Gleichung identifizieren.
- Der Übergang von Quantenmechanik zu Feldtheorie
Mit den Mitteln der Quantenmechanik hatten wir folgende Formel für die Zeitentwicklung gefunden:
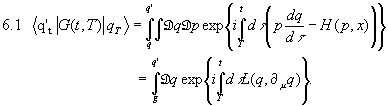
Anmerkung zur Notation: Im folgenden werden wir für die Übergangsamplitude 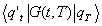 verkürzend
verkürzend 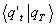 schreiben.
schreiben.
Uns stellt sich jetzt die Aufgabe, 6.1 in die Feldtheorie hinüberzuretten.
Bei der Herleitung von Formel 6.1 wurde vor allem folgende Formel benützt:
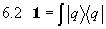 .
.
In dem Gaußschen Integral
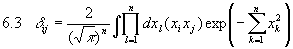
ersetzen wir die Variable 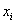 durch die Funktion
durch die Funktion 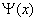 , hier als diskretisierte Zahl begriffen.
, hier als diskretisierte Zahl begriffen.
Dann erhalten wir folgenden Ausdruck für eine
1:
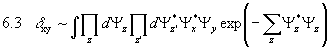 .
.
Machen wir nun vollends den Übergang zu Funktionen 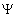 , so erhalten wir mit
, so erhalten wir mit 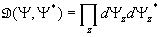 :
:
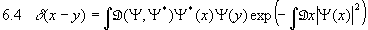 .
.
Schreibt man nun wie in der Quantenmechanik statt 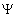 den Ket
den Ket 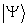
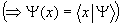 , so gilt:
, so gilt:
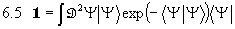
Damit muß man nun alle Schritte, die zum Pfadintegral führten, wiederholen und erhält für den Übergang:
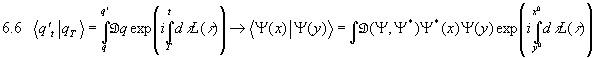
Vergleiche dies mit 3.1. Um zur Berechnung von Korrelationsfunktionen auf die Ergebnisse aus Kapitel 3 zurückgreifen zu können, definieren wir als erzeugendes Funktional
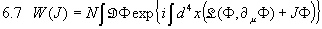
Mit der Normierungskonstanten
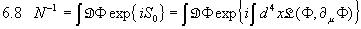 .
.
Damit erreichen wir insbesondere W(0)=1. Ebenso verschwinden eventuelle unendliche Faktoren.
- Das freie skalare Feld in Pfadintegralbehandlung
Als erste Anwendung des Pfadintegralformalismus werden wir das freie skalare Feld behandeln und dessen Propagatoren herleiten, d.h. die Korrelationsfunktion 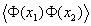 bestimmen. Wir werden dazu 6.7 benutzen. Dies ergibt die Wirkung
bestimmen. Wir werden dazu 6.7 benutzen. Dies ergibt die Wirkung
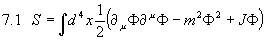 .
.
Für J=0 ergibt sich offensichtlich wieder die Wirkung für das freie skalare Feld. Physikalisch entspricht dies dem freien skalaren Feld, das zusätzlich noch einer äußeren Quelle (einem Kraftfeld) unterliegt. Nun stellt sich noch das Problem, daß wir nicht wissen, welchen definierten (!) Zustand wir unserer Rechnung zu Grunde legen dürfen. Wir erhalten diesen über folgende Überlegung. Unter allen möglichen Zuständen muß es einen der geringsten Energie geben, den wir Grundzustand nennen und mit dem wir rechnen wollen. Wir werden daher 6.7 als die Zeitentwicklungsamplitude 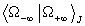 für einen Grundzustand
für einen Grundzustand 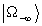 für
für 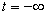 in der Vergangenheit zu einem Grundzustand
in der Vergangenheit zu einem Grundzustand 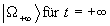 für obige Wirkung betrachten. Zudem ist wegen 6.8 gewährleistet, daß die Zeitentwicklungsamplitude des ungestörten Grundzustandes gleich 1 ist, was mit den grundlegenden physikalischen Überlegungen übereinstimmt. Wir erhalten daher mit 7.1:
für obige Wirkung betrachten. Zudem ist wegen 6.8 gewährleistet, daß die Zeitentwicklungsamplitude des ungestörten Grundzustandes gleich 1 ist, was mit den grundlegenden physikalischen Überlegungen übereinstimmt. Wir erhalten daher mit 7.1:
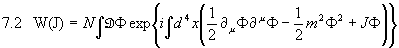 .
.
Dies ist das zu lösende Pfadintegral. Leider ist der Integrand, da rein imaginär, oszillierend und das Pfadintegral ist û mathematisch û nicht wohldefiniert. Um dem abzuhelfen und doch noch an eine Lösung zu gelange, gibt es zwei prinzipielle Möglichkeiten:
- Man schreibt einen Konvergenzfaktor
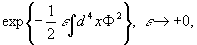 in das Integral oder
in das Integral oder
- transformiert in den euklidischen Raum, indem man
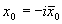 und
und 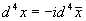
setzt.
Wir werden hier zunächst die erste Möglichkeit weiter verfolgen und betrachten
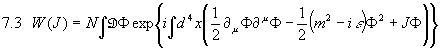
Dies werden wir durch vierdimensionale Fourier-Transformation im Impuls-Raum lösen. Dazu definieren wir die vierdimensionale Fourier-Transformation durch
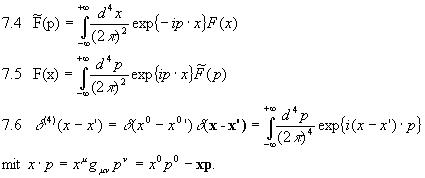
Der Exponent von 7.3 wird dann
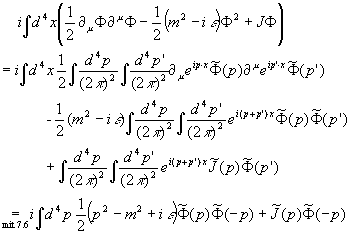
Schreibt man dies mit 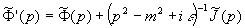 um, so erhält man:
um, so erhält man:
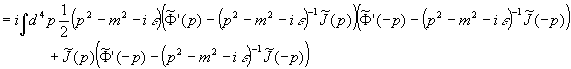
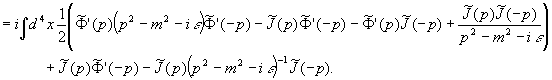
Weil 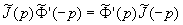 , wie sich aus der Rechnung ergibt, lautet das Endresultat unserer Umformungen:
, wie sich aus der Rechnung ergibt, lautet das Endresultat unserer Umformungen:
 .
.
Damit haben wir die Terme in  und J separiert. Besonders angenehm ist, daß
und J separiert. Besonders angenehm ist, daß 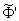 und
und 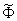 sich im Funktionenraum nur um eine Konstante unterscheiden und somit
sich im Funktionenraum nur um eine Konstante unterscheiden und somit 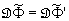 ist. Damit haben wir:
ist. Damit haben wir:
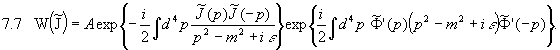
Zurücktransformation des zweiten Faktors liefert:
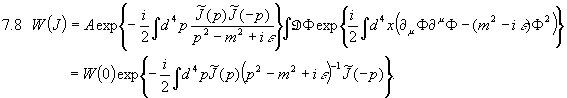
Einsetzen der Fouriertransformierten von 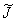 führt auf
führt auf
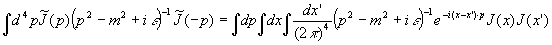 .
.
Es folgt
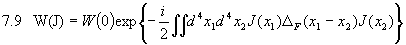
mit dem Feynman-Propagator
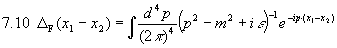 .
.
Beachte hierbei 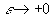 . Wir wollen nun die Techniken aus Kapitel 3 benützen und damit die fundamentale Bedeutung des Feynman-Propagators erhellen. Wir erhalten die Korrelationsfunktionen (Greenschen Funktionen) des Feldes analog zu 3.4 durch:
. Wir wollen nun die Techniken aus Kapitel 3 benützen und damit die fundamentale Bedeutung des Feynman-Propagators erhellen. Wir erhalten die Korrelationsfunktionen (Greenschen Funktionen) des Feldes analog zu 3.4 durch:
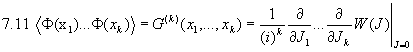
Für die Korrelation des Feldes an zwei Orten erhält man daher:
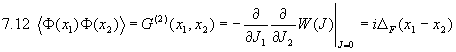 .
.
Der Feyman-Propagator ist also im Wesentlichen die Greensche Funktion des Feldes 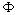 , d.h.
, d.h.
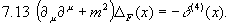
Mit dem Wickschen Theorem 3.9 können wir dann auch sofort kompliziertere Greensche Funktionen des Feldes berechnen, z.B.:
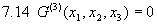 und
und

Damit können wir nun endgültig eine physikalische Interpretation des Feynman-Propagators geben:
D F propagiert die Lösungen der Klein û Gordon û Gleichung. Man kann nun über die Betrachtung des Grenzwertparameters ie zeigen, daß D F die Lösungen positiver Energie (p0>0), die als Teilchenzustände interpretiert werden, in der Zeit vorwärts propagiert, während die Lösungen negativer Energie, die als Antiteilchenzustände intepretiert werden, in der Zeit rückwärts (!) propagiert werden. Für das komplexe skalare Feld erhält man ohne große Umstände den gleichen Propagator. Wir dürfen daher G(2)(x,y) als die Zeitentwicklungsamplitude eines Teilchens (z.B. p 0-Meson) der Masse m2 intepretieren, das von x nach y geht.
Nun verfolgen wir die zweite Möglichkeit weiter:
Die Transformation in den euklidischen Raum erfolgt durch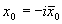 und
und 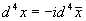 , und es folgt
, und es folgt
 . Die euklidischen Variablen werden durch den Querstrich gekennzeichnet.
. Die euklidischen Variablen werden durch den Querstrich gekennzeichnet.
Wir erhalten als erzeugendes Funktional:
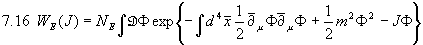
Die Übertragung unserer Ergebnisse aus Kapitel 1, insbesondere Formel 1.7, ermöglicht uns, da wir mit der oberen Rechnung praktischerweise auch das Inverse des Operators 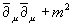 bestimmen könnten, sofort die Lösung anzugeben:
bestimmen könnten, sofort die Lösung anzugeben:
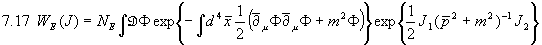
Damit erhalten wir als Propagator
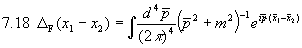
Dabei haben wir uns die euklidische Fouriertransformation passend definiert. Wir haben jetzt allerdings noch das Problem, wie wir von der imaginären Zeit auf die Antwort für reelle Zeiten zurückschließen können. Die Antwort darauf liefert die sogenannte Wickrotation: Wir setzen 7.18 analytisch ins Imaginäre fort.
Da die Pole von 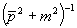 auf der imaginären p0-Achse liegen und dies für die weitere Diskussion unangenehm ist, betrachten wir statt dessen
auf der imaginären p0-Achse liegen und dies für die weitere Diskussion unangenehm ist, betrachten wir statt dessen
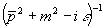 .
.
Damit erhalten wir Pole bei
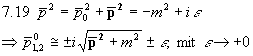
Da die Pole außerhalb der geschlossenen Kontur
C=CI+CII+CIII+CIV
liegen, gilt nach dem Residuensatz:
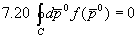
mit
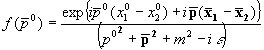
Die Integrale über die Viertelkreise CII und CIV verschwinden für 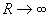 . Siehe hierzu Anhang C. Es folgt:
. Siehe hierzu Anhang C. Es folgt:
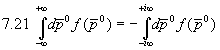 .
.
Indem man die für reelle euklidische Zeiten gefundene Lösung analytisch in die komplexe Ebene fortsetzt, erhält man die Lösung für reelle minkowskische Zeiten. Anschaulich bedeutet dies, daß man die Achsen um 90ø im Uhrzeigersinn rotiert (bei der Rücktransformation gegen den Uhrzeigersinn, wesentlich ist, daß man bei der Rotation nicht auf Singularitäten stößt). Deshalb der Ausdruck Wickrotation.
Führen wir nun auf der rechten Seite der Gleichung die Rücktransformation aus, d.h.
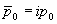 und
und 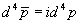 , so erhalten wir
, so erhalten wir
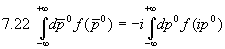
und deswegen
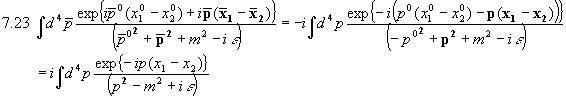
Wir haben somit gezeigt, daß die beiden Herangehensweisen an das Problem das gleiche Ergebnis liefern, und gleichzeitig auch noch eine Möglichkeit gefunden, um Ergebnisse aus dem euklidischen Raum in den minkowskischen und umgekehrt zu übersetzen: die Wickrotation.
Damit ist unsere Behandlung des freien skalaren Feldes abgeschlossen.
Anhang:
A. Das Wicksche Theorem:
Man findet das Wicksche Theorem in zwei Formen: Zum einen erscheint es bei dem Problem der Zeitordnung von Operatoren, zum anderen erhält man es aus der Betrachtung des Gaußschen Integrals. Wir geben hier noch einen kurzen Einblick in das Wicksche Theorem für Operatoren.
Für Operatoren ist es nicht selbstverständlich, daß sie normalgeordnet sind, d.h. alle Erzeuger im Produkt stehen links und alle Vernichter rechts, so daß für ein normalgeordnetes Operatorprodukt AB immer gilt: 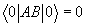
Wir definieren daher eine Normalordnung :AB: des Operatorproduktes durch:
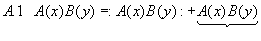
wobei offenbar gilt:
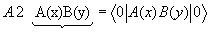
Die Paarung 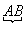 entspricht also dem Vakuumerwartungswert von AB.
entspricht also dem Vakuumerwartungswert von AB.
Das Wicksche Theorem lautet dann:
A.3:
"...the ordinary product of linear operators is equal to the sum of all the corresponding normal products with all possible pairings, including the normal product without pairings:
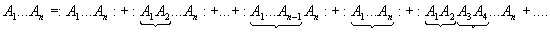 " (Boguliubov 1980, S. 159). Zum Beweis siehe dort. Gemeinhin findet an das Wicksche Theorem so für das zeitgeordnete Operatorprodukt formuliert. Siehe dazu z. B. Köpp, 1997, Kapitel 7.
" (Boguliubov 1980, S. 159). Zum Beweis siehe dort. Gemeinhin findet an das Wicksche Theorem so für das zeitgeordnete Operatorprodukt formuliert. Siehe dazu z. B. Köpp, 1997, Kapitel 7.
Die in 3.8 gegebene Formulierung des Wickschen Theorems für Gaußintegrale ist nur ein Spezialfall der oben angegebenen allgemeinen Form des Theorems.
B. Einige nützliche Formeln zu Gaußschen Integralen und Propagatoren:
Einige Gaußintegrale:
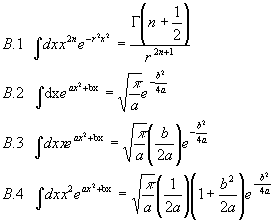
Die Schrittfunktionen:
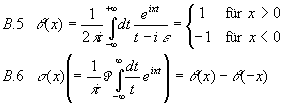
(
P zeigt den Hauptwert des Integrals an.)
Kausale Greensche Funktion für das skalare Feld:
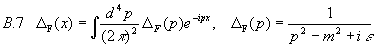
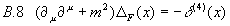
Man erhält nun die retardierten und avancierten Greenschen Funktionen
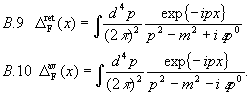
Interessant sind auch die Greenschen Funktionen im Impulsraum. Schon aus 7.8 kann man ersehen, daß in ihnen die Impulserhaltung manifest wird, denn wir erhalten ohne große Umschweife
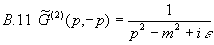 .
.
Wir setzen daher für die Greenschen Funktionen im Impulsraum:
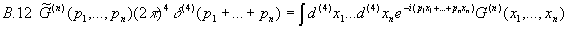
Damit ist sichergestellt, daß 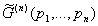 nur dann definiert ist, wenn
nur dann definiert ist, wenn 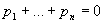 gilt. Damit ist sowohl die klassische Energie- als auch Impulserhaltung gesichert.
gilt. Damit ist sowohl die klassische Energie- als auch Impulserhaltung gesichert.
Im Rahmen des Operatorformalismus werden die Greenschen Funktionen über den Zeitordnungsoperator T definiert. Es gilt für den Vakuumserwartungswert:
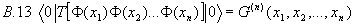 .
.
Aus dem Pfadintegralformalismus ergibt sich die Zeitordnung ganz normal.
C Beweis für das Verschwinden der Integrale über CII und CIV
Das einzig interessante Integral ist, wie durch die Rechnung klar wird, das über CII . Wir betrachten daher:
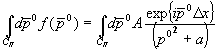 .
.
Mit der Ersetzung 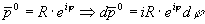 erhält man:
erhält man:
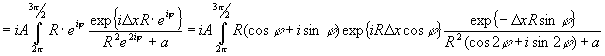 Weil der
Weil der 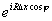 -Term rein oszillatorisch ist und für
-Term rein oszillatorisch ist und für 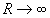 immer stärker oszilliert, wird der Rest des Integranden zuverlässig weggemittelt. Das Integral über CII verschwindet also trotz der reellen Exponentialfunktion, die gegen Unendlich strebt. Gleiches gilt auch für das Integral über CIV, doch dort sorgt schon die Exponentialfunktion für Konvergenz gegen Null.
immer stärker oszilliert, wird der Rest des Integranden zuverlässig weggemittelt. Das Integral über CII verschwindet also trotz der reellen Exponentialfunktion, die gegen Unendlich strebt. Gleiches gilt auch für das Integral über CIV, doch dort sorgt schon die Exponentialfunktion für Konvergenz gegen Null.
D Zu den natürlichen Einheiten
Mit 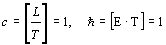 können wir über E=mc2 alle Einheiten auf die Dimension der Masse zurückführen und erhalten:
können wir über E=mc2 alle Einheiten auf die Dimension der Masse zurückführen und erhalten: 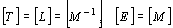 .
.
Damit haben Raum und Zeit die Dimension û1, Energie und Masse +1 und Geschwindigkeit und Wirkung 0. Die Lagrangedichte hat also im n-dimensionalen Raum (der "natürlichen" Dimension ûn), die Dimension +n. Dies wird wichtig, wenn man zu Renormierungsproblemen kommt, wo die Renormierbarkeit der Theorie nur dadurch gewährleiste ist, daß die Dimension der Lagrangedichte nie größer als die (normale) Dimension des betrachteten Raumes sein darf.
E Das komplexe freie skalare Feld
Die Lagrangedichte des komplexen freien skalaren Feldes ist
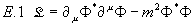 .
.
Es ist unter der kontinuierlichen Transformation 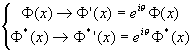 invariant.
invariant.
Der nach dem Noethertheorem erhaltene Noetherstrom (d.h. 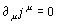 ) lautet
) lautet
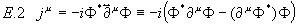 .
.
Die erhaltene Ladung
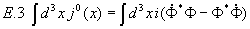
ist die gewöhnliche elektrische Ladung. Damit ist gezeigt, daß das komplexe skalare Feld Ladung trägt. Indem man nun mit Hilfe von 1.8 alle obigen Schritte wiederholt, erhält man den gleichen Propagator und kann die oben gemachten Aussagen auf alle (pseudoskalaren) spinlosen Bosonen (z.B. Pionen) übertragen. Allerdings trägt eine nicht-selbstwechselwirkende Theorie für geladene Teilchen nicht sehr weit.
Literatur:
N.N. Bogoliubov, D.V. Shirkov, Quantum Fields, The Benjamin/Cummings Pub. Corp., Inc. 1983
N.N. Bogoliubov, D.V. Shirkov, Introduction to the Theory of Quantized Fields, 3rd ed., Wiley 1980
P.H. Frampton, Gauge Field Theories, Frontiers in Physics, Addison Wesley, 1986
E.M. Henley, W. Thirring, Elementare Quantenfeldtheorie, BI-Wissenschaftsverlag, 1975
M. Kaku, Quantum Field Theory, a modern introduction, Oxford University Press, 1993
G. Köpp, F. Krüger, Einführung in die Quantenelektrodynamik, Teubner, 1997
T. Kugo, Eichtheorie, Springer, 1997
I. Montvay, G. Münster, Quantum Mechanics on the Lattice, Cambridge University Press, 1994
J.W. Negerle, H. Orland, Quantum Many-Particle System, Frontiers in Physics, Addison Wesley, 1987
P. Ramond, Field Theory: a modern primer, 2nd ed., Frontiers in Physics, Addison Wesley, 1990
L.S. Schulman, Techniques and Applications of Path Integrals, Wiley, 1981
F. Schwabl, Quantenmechanik für Fortgeschrittene (QM II), Springer, 1997
J. Zinn-Justin, Quantum Field Theory and Critical Phenomena, Oxford University Press, 1989
![]()
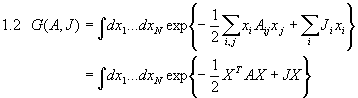
![]()
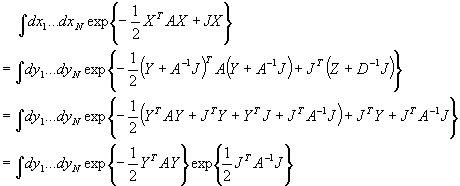
![]() und mit RY=Z und daher
und mit RY=Z und daher ![]() erhalten wir:
erhalten wir: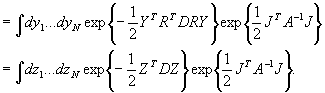
![]() .
.![]() erhalten wir als Endergebnis:
erhalten wir als Endergebnis: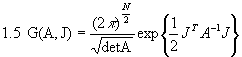 .
.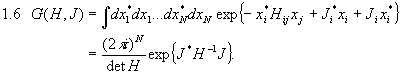
![]() (
(![]() ) ersetzen. Um ein konvergentes Ergebnis zu erhalten, müssen wir das richtige Maß benützen und den vorher unterdrückten Faktor
) ersetzen. Um ein konvergentes Ergebnis zu erhalten, müssen wir das richtige Maß benützen und den vorher unterdrückten Faktor ![]() wieder in das Integral schreiben. Wir erhalten dann die Formeln:
wieder in das Integral schreiben. Wir erhalten dann die Formeln: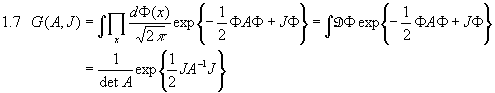
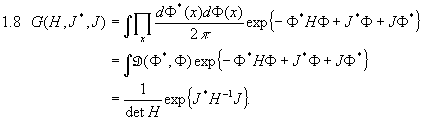
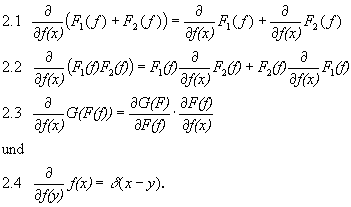
![]()
![]() gewinnen ließe.
gewinnen ließe.![]()
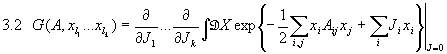
![]() im kontinuierlichen Fall. Mit 1.5 erhalten wir als Endergebnis
im kontinuierlichen Fall. Mit 1.5 erhalten wir als Endergebnis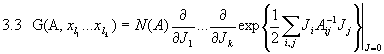
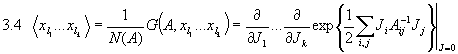 .
.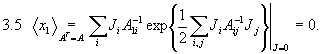
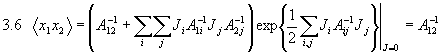 .
.![]() natürlich
natürlich ![]() . Für k=3:
. Für k=3: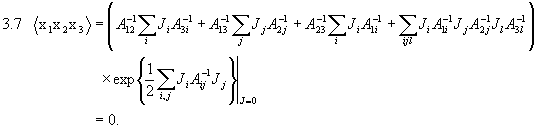
![]() .
. .
.![]()
![]()
![]() .
.![]() über, so erhält man die übliche Form der Klein û Gordon û Gleichung:
über, so erhält man die übliche Form der Klein û Gordon û Gleichung: ![]() .
.![]() eine skalare Funktion und man unterscheidet zwei Fälle: Ist
eine skalare Funktion und man unterscheidet zwei Fälle: Ist ![]() reell, so trägt das Teilchen keine Ladung , für komplexe
reell, so trägt das Teilchen keine Ladung , für komplexe ![]() ist eine Ladung dagegen erlaubt. Wir behandeln im weiteren nur das reelle skalare Feld.
ist eine Ladung dagegen erlaubt. Wir behandeln im weiteren nur das reelle skalare Feld.![]() definiert. Darüber gelangt man zur LagrangeûDichte
definiert. Darüber gelangt man zur LagrangeûDichte ![]() .
.![]()
![]() mit den Nebenbedingungen
mit den Nebenbedingungen ![]() erhält man wiederum die Euler-Lagrange-Gleichungen für
erhält man wiederum die Euler-Lagrange-Gleichungen für ![]() :
:![]()
![]() konjugierte Impuls-Feld lautet dann
konjugierte Impuls-Feld lautet dann![]()
![]() .
.![]()
![]()
![]()
![]() folgt mit den Euler û Lagrange - Gleichungen für das freie skalare Feld aus 5.6:
folgt mit den Euler û Lagrange - Gleichungen für das freie skalare Feld aus 5.6:![]() .
.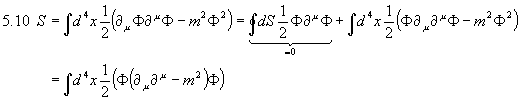
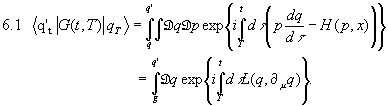
![]() verkürzend
verkürzend ![]() schreiben.
schreiben.![]() .
.![]()
![]() durch die Funktion
durch die Funktion ![]() , hier als diskretisierte Zahl begriffen.
, hier als diskretisierte Zahl begriffen.![]() , so erhalten wir mit
, so erhalten wir mit ![]() :
:![]() .
.![]() den Ket
den Ket ![]()
![]() , so gilt:
, so gilt:![]()
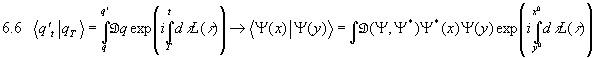
![]()
![]() .
.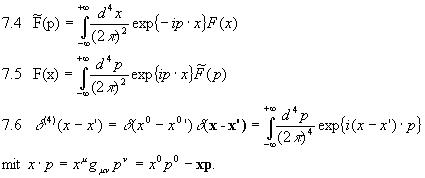
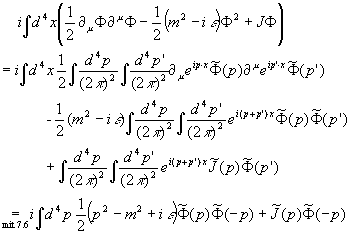
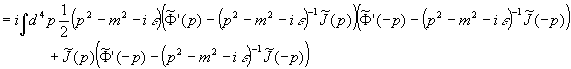
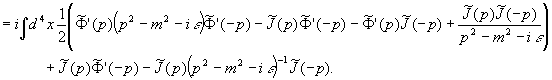
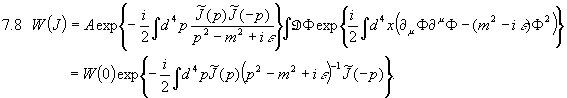
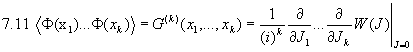
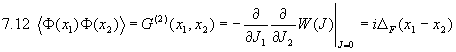 .
.
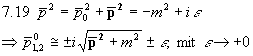
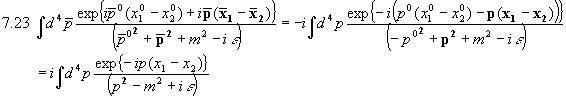
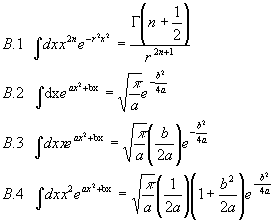
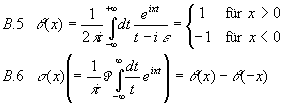
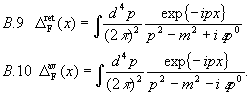
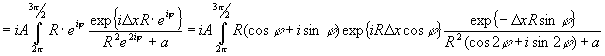 Weil der
Weil der