



Next: Maximum likelihood approximation
Up: The likelihood model of
Previous: Measurements in quantum theory
Contents
From now on we will
consider a quantum mechanical canonical ensemble at temperature 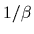 .
Such a system is described by a density operator
.
Such a system is described by a density operator
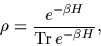 |
(15) |
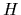 denoting the Hamiltonian of the system.
Specifically, we will focus on repeated measurements
of a single particle in a heat bath of temperature
denoting the Hamiltonian of the system.
Specifically, we will focus on repeated measurements
of a single particle in a heat bath of temperature 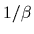 with sufficient time between measurements
to allow the heat bath to reestablish the canonical density operator.
For (non-degenerated)
particle coordinates
with sufficient time between measurements
to allow the heat bath to reestablish the canonical density operator.
For (non-degenerated)
particle coordinates 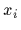 the likelihood for
the likelihood for 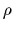 becomes the thermal expectation
becomes the thermal expectation
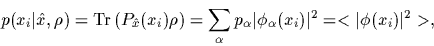 |
(16) |
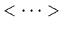 denoting the thermal expectation with probabilities
denoting the thermal expectation with probabilities
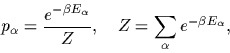 |
(17) |
and energies and orthonormalized eigenstates
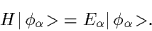 |
(18) |
In particular, we will consider a hermitian Hamiltonian of the
standard form
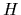 =
= 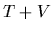 ,
with kinetic energy
,
with kinetic energy 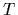 ,
being
,
being 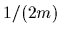 times the negative Laplacian
times the negative Laplacian 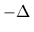 for a particle with mass
for a particle with mass 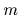 (setting
(setting 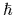 =
= 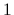 ),
and local potential
),
and local potential
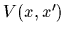 =
=
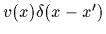 .
Thus, in one dimension
.
Thus, in one dimension
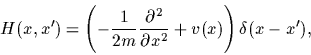 |
(19) |
where the 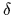 -functional is usually skipped.
-functional is usually skipped.
For 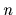 independent position measurements
independent position measurements 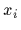 the likelihood for
the likelihood for 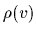 , and thus for
, and thus for 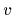 , becomes
(writing now
, becomes
(writing now
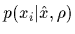 =
=
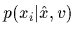 )
)
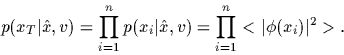 |
(20) |
We remark that it is straightforward to allow
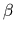 to vary between measurements.
to vary between measurements.




Next: Maximum likelihood approximation
Up: The likelihood model of
Previous: Measurements in quantum theory
Contents
Joerg_Lemm
2000-06-06
![]() .
Such a system is described by a density operator
.
Such a system is described by a density operator
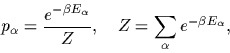
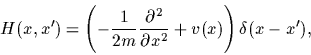
![]() independent position measurements
independent position measurements ![]() the likelihood for
the likelihood for ![]() , and thus for
, and thus for ![]() , becomes
(writing now
, becomes
(writing now
![]() =
=
![]() )
)